From planar graphs to higher dimensions
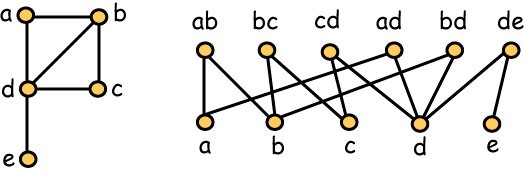
A graph and its inclusion poset
Planar graphs is a widely studied class of graphs which history starts in the 19th century. However, in the early 90's W. Schnyder found a surprising caracterization of these graphs [Sch]. A graph $G$ is planar if and only if its inclusion poset has dimension at most 3. The inclusion poset of a graph $G=(V,E)$ is the poset on $V\cup E$ such that $x\prec y$ iff $x$ is an end vertex of $y$, which is an edge. The dimension of a poset $\prec$ is the minimum number of linear orders $\prec_1,\ldots,\prec_k$ such that $x \prec y$ iff $x\prec_i y,\, \forall i\in\{1\ldots k\}$.

Example of a Schnyder wood
The tools introduced in that proof (the Schnyder woods) yield to many combinatorial properties, such as bijections between (oriented) planar graphs and contact system of polygons, TD-Delaunay triangulations, or Dyck words. They also appear in various computer science applications such as graph drawing, succinct encoding, graph spanners, etc.
This proposal aims at generalizing these properties to higher dimensional objects: simplicial complexes whose inclusion poset has dimension $d=4$. For such simplicial complex the inclusion poset relates vertices, edges, triangles, and tetrahedrons. The case $d=1$ is the single vertex, the case $d=2$ corresponds to the graphs that are the union of disjoint paths. The case $d=3$ corresponds to the simplicial complexes whose edges induce a planar graph, and whose triangles correspond to some triangular faces of that planar graph [BT]. For higher $d$, P. Ossonna de Mendez [Oss] proved that such simplicial complexe $C$ linearly embeds in $\mathbb{R}^{d-1}$ without crossings.
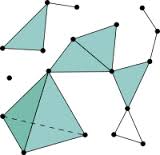
Linear embedding without crossings
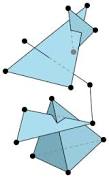
Linear embedding with crossings
Some properties of planar graphs seem related to the dimension of the incidence poset. This raises natural questions about extending these properties to the case $d=4$:
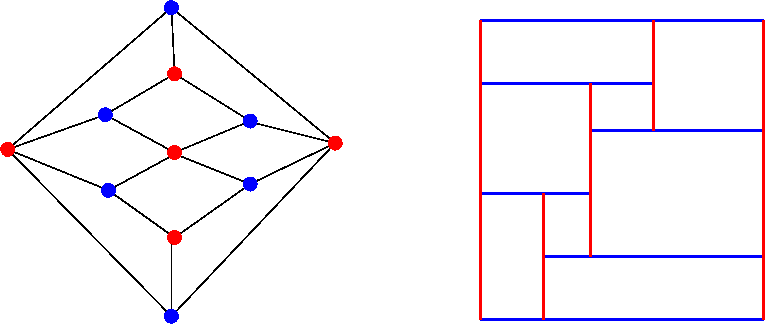
Bipartite planar graph and a corresponding contact system of segments
Every bipartite planar graph can be represented by a system of axis aligned segments in contact [FPP].
In such representation each vertex corresponds to a segment, and two adjacent vertices should have their corresponding segments that touch, here crossings of segments are not allowed.
Consider a contact system $S$ of axis aligned rectangles in $\mathbb{R}^3$, such that for any two touching rectangles their intersection is exactly one side of these rectangles. The simplicial complex $C(S)$ obtained from $S$ has one vertex for each rectangle, an edge for each pair of touching rectangle, and a triangle for each triplet of intersecting rectangles. One can show that such $C(S)$ has dimension at most $4$. It would be interesting to know if every tripartite complex with dimension $d=4$ admits such representation.
[BT] G. Brightwell and W.T. Trotter, The order dimension of planar maps, SIAM J.Disc. Math. 10 (1997), 515-528.
[FPP] H. de Fraysseix, J. Pach, and R. Pollack, How to draw a planar graph on a grid, Combinatorica 10(1), (1990), 41-51.
[Oss] P. Ossona de Mendez, Geometric realization of simplicial complexes, LNCS 1731 (1999), 323-332.
[Sch] W. Schnyder, Planar graphs and poset dimension, Order 5 (1989), 323-343.
