Lessons learned from Summary Reject phase#

IJCAI-PRICAI 2020 introduced a new procedure in the review process for
its main track: a phase of summary reject before the standard review
process (aka full review). Here is a brief report on how it went and
on the pros and cons of the way I implemented it.

1. Preliminaries

The main track had received 5147 submissions. After having discarded
papers with obvious violation of the submission guidelines (mainly
overlength papers and broken anonymity), 4804 entered the summary
reject phase. From those 4804 papers, only 4734 still in the system
were used for the analyses in this report. The missing papers are
either papers that have been detected as violating the submission
guidelines during the review process or papers that have been
withdrawn by the authors.

The IJCAI program committee of the main track was composed of PC
members (PCs), who traditionally write reviews, senior PCs (SPCs), who
traditionally monitor discussions and suggest accept/reject decisions,
and area chairs (ACs), who traditionally take the accept/reject
decision. In 2020, the roles of SPCs and ACs were augmented by a
participation in the summary reject phase (not the PCs). Each of the
4804 papers was assigned 7 or 10 SPCs (depending on the area and the
ratio #papers/#SPCs in each area). Each SPC received up to 42 papers
(average 38). They were asked to spend 5 to 10 minutes on each paper,
to vote whether they think the paper should (yes-vote) or should not
(no-vote) go into full review, and optionally (but strongly
recommended) add a sentence of justification. Each AC was in charge of
up to 68 papers (average 52) for which they had to decide whether the
paper would go into full review or not. They were free to take their
decision based on the votes only, or after having a look at the paper
themselves.

2. What was not expected from this new process

• The summary-reject phase has made the process of inviting SPCs more
  challenging. Many of them were scared by this new feature they've
  never seen before. As I didn't know the amount of papers I would
  have to send to each SPC I presented it as "a big day of
  work". (With 40 papers and 8 hours of work, it allows 12 minutes per
  paper.) To avoid that too many invited SPCs decline, I relaxed the
  original condition that a couple of sentences of justification of
  the vote was required. Once this condition relaxed, the number of
  people declining the invitation to be an SPC significantly
  dropped. However, it had an effect that I had not anticipated: at
  the time of summary-reject decisions, ACs didn't always have enough
  written material from SPCs to write the justification for summary
  rejection. To avoid that some authors receive text justifying the
  summary reject and others not, I decided not to send any of the
  summary-reject feedbacks from ACs.
• Once the summary-reject notifications went out, a big wave of
  complaints hit me. They had two origins. One was due to the lack of
  written reason for rejection. Even though it had been extensively
  explained (CFPs, video, etc.), many authors totally overlooked this
  point. The second reason was a misunderstanding (probably by lack of
  communication from me) of what summary reject was meant for. As we
  will see later, summary reject doesn't mean low-quality paper. It
  often means that the paper is too incremental or that the topic is
  too narrow for a general audience conference such as IJCAI, and that
  it would be more suited to its related specialized conference (eg,
  ICAPS, AAMAS, SAT, KR, CP, etc.).
• I thought that notifying summary rejected papers one month after
  submission was good because authors wait three times less than in
  standard full-review process. They are then able to submit to other
  conferences with deadlines between end of February and end of
  April. But an unexpected side effect has been that some PCs/SPCs,
  who were also authors of summary-rejected papers, resigned from
  their PC/SPC commitment because they were upset.

3. Personal opinion after having observed the summary reject phase and the full review phase

In the summary-reject phase, the words "lack of novelty" or "too
incremental" were frequently used, many more often than in standard
reviews. Weak experimental evaluation was also frequently used, but
not sure it was more used than in full reviews. Finally, "weak
technical contribution" or "flaws in the technical contribution" are
reasons that seem to have been used significantly less often than in
full reviews.

Why such differences? I see several reasons:

• when you spend 10 minutes on a paper you don't have time to detect
  errors.
• when you scroll 40 papers --summary-reject phase-- instead of half a
  dozen --full review phase, you have a more global view on what is
  incremental in a mainstream topic and what is innovative.
• SPCs are in general more senior than PCs, so they are more sensible
  to the big picture, the novelty, than PCs.
• In the summary-reject phase, papers were assigned to SPCs by
  subject-areas matching whereas in the full review phase they were
  assigned to PCs mainly following their bids. As a consequence, a
  paper in a narrow topic had great chances to be reviewed by PCs from
  this narrow topic, who will most probably not report the
  narrow/incremental aspect. (We had anticipated that bias by
  assigning an extra PC to each paper based on main subject area
  instead of bids, but these PCs usually didn't influence the
  decision, considering themselves as less expert.) On the contrary,
  SPCs were in charge of papers belonging to their area in a broader
  sense.

4. Statistical analysis on the outcome of this two-phases process

For this analysis we only consider the 4734 papers that were neither
detected as violating the guidelines nor withdrawn by authors during
the review process. 2268 of these papers were proposed for summary
reject and 2466 for full review. In order to be able to fully assess
the correlation of the summary-reject decisions with the final
decisions, I randomly selected 100 papers from the summary rejected
papers and I sent them into full review. I will call these papers the
"lottery winners". To avoid any bias, I assigned the lottery winners
to an SPC and an AC different from those assigned during the
summary-reject phase. There are thus 2466 + 100 = 2566 papers that
reached the end of the full-review phase. Among the 100 lottery
winners, 8 have been accepted, which represents 8% of misclassified
papers if we consider the full-review phase as flawless.

4.1. Correlation between SPC votes and acceptance rate

As mentioned above, deciding the quality of a paper is a
multi-criteria decision problem and we cannot claim that full review
decisions are the perfect outcome. (See this interesting evaluation of
the lack of robustness of standard reviewing processes performed by
NeurIPS a few years ago
http://blog.mrtz.org/2014/12/15/the-nips-experiment.html, or the more
recent ESA experiment
https://cacm.acm.org/blogs/blog-cacm/248824-how-objective-is-peer-review/fulltext.)
However, in the absence of any other measure of quality (in 10 years
from now we could see how much each papers got cited), the only way I
can assess the quality of the summary-reject phase is by measuring its
correlation with the final decisions.

Given a paper, I will denote by #yeses (resp. #noes) the number of
yes-votes (resp. no-votes) that this paper received from SPCs. Each
paper was assigned 7 or 10 SPCs depending on the area, and not all
SPCs entered their votes on time. Hence, at the end of the
summary-reject phase, papers had received from 4 votes --only 5 papers
are in this case-- to 10 votes --951 papers.

I first analyzed how much the votes from SPCs in the summary-reject
phase are correlated to the acceptance rate in the full-review phase.
Given the 2566 papers that reached the end of the full review phase
(let us call this set S), let X be the vector containing all the
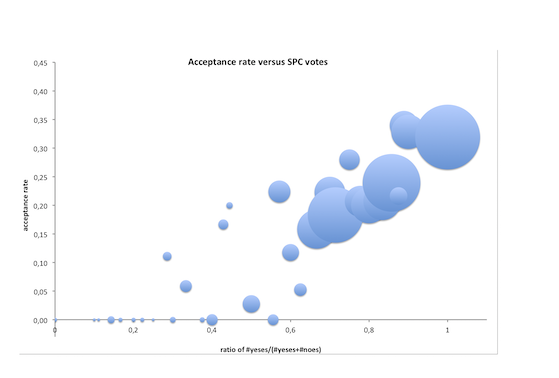
possible ratios of yes-votes: #yeses/(#yeses+#noes). There are 33
possible ratios, going from 0 to 1. I denote by S[i] the subset of
papers from S having the ratio X[i] of yes-votes. The vector Y is
defined in such a way that Y[i] is the acceptance rate in S[i]. For
instance, the 23rd possible ratio of yes-votes is X[23]=0.7. The set
S[23] of papers that obtained a ratio of yes-votes equal to 0.7
contains 112 papers, among which 25 got accepted, that is, Y[23]=0.22.

Spearman's correlation between X and Y is 0.85. Spearman's correlation
measures the statistical dependence between the rankings in two
vectors of values and takes values between -1 and 1. A value of 0
means no correlation at all between X and Y, whereas value 1
(resp. -1) means a perfectly monotone (resp. anti-monotone)
correlation. A value of 0.85 shows that the ratio of SPC votes
correlates reasonably well with final decisions. In order to assess
the robustness of SPC votes depending on the number of votes on a
paper, I recomputed Spearman's correlation on vectors X_(k) and Y_(k),
where S_(k) is the subset of S containing all papers with at most k
votes. Spearman's correlation grows from 0.65 for S_(5) to 0.85 for
S_(10). (S_(4) has a Spearman's correlation of 1 but 5 papers is a too
small sample.) This increase of Spearman's correlation when the
number of SPC votes increases shows that, as expected, more votes
means better prediction.

A weakness of this analysis is that two subsets S[i] and S[j] have the
same weight on the final result, whatever their size. S[i] could
represent 400 papers whereas S[j] represents only 10 papers. To avoid
this bias, I computed the weighted Spearman's correlation between X
and Y, where the distance between X[i] and Y[i] is weighted by
|S[i]|. The overall Spearman's correlation between X and Y goes from
0.85 in the non-weighted case to 0.96 in the weighted case. It also
significantly increases for all subsets S_(k), but the dependence on k
is no longer obvious: 0.93 for S_(5) and at least 0.95 for all other
values of k.

Figure 1 displays Y for each value of X. The size of the bubble
representing Y[i] is proportional to the number of papers in S[i].

4.2. Comparison of SPC votes and AC decisions

The second point I wanted to assess is the added value of the AC
summary-reject decision compared to the SPC votes. In the following,
when the ratio #yeses/(#yeses+#noes) for a paper is smaller than the
threshold 0.5, we say that the SPCs want to summary reject the paper,
when #yeses/(#yeses+#noes) is greater than or equal to the threshold
0.5 we say that SPCs want to send the paper into full review.

We then have four categories of papers to consider:

• (YES-YES) SPCs and AC agree to send the paper into full review,
• (NO-YES) SPCs want to summary reject and AC sends into full review,
• (YES-NO) SPCs want to send into full review and AC summary rejects,
  and
• (NO-NO) SPCs want to summary reject and AC summary rejects.

The following table summarizes the cardinalities of each category. As
YES-NO papers and NO-NO papers were proposed by their AC for summary
rejection, their only witnesses in the full-review phase are the
lottery winners (middle column). For those categories in which papers
went through the full-review phase, numbers in brackets report the
number of accepted papers in the given category.

Not surprisingly, the large majority of papers (2442) are in category
YES-YES. The acceptance rate is 23.8%. This is by far the highest rate
of all categories.

There are 24 papers that the SPCs wanted to summary reject and that
the AC sent to full review. However, only one of them has finally been
accepted, which means that the AC was "right" against SPCs in 4.2% of
the cases. It is extremely far from the 23.8% of the YES-YES
category. It tends to show that the decision to override the SPCs
inclination was a bad decision.

The evaluation of the categories YES-NO and NO-NO is based on the
lottery winners only because, by definition, the other papers in these
categories have been summary rejected by their AC. Among the 42
papers that the SPCs wanted to send to full review and that the AC
summary rejected (YES-NO papers), 4 have been accepted. This means
that the SPCs were "right" against AC in 9.5% of the cases. It is
lower than the 23.8% of the YES-YES category, but significantly higher
than the NO-YES category. In addition, bear in mind that these 4
YES-NO papers are among 42 lottery winners representing 1067 other
YES-NO papers, whereas the single NO-YES paper is among all the
papers.

Finally, among the 58 papers that both SPCs and AC wanted to summary
reject, 4 were accepted (6.9%). It is noticeable that even this
category where SPCs and AC agreed to summary reject has a higher
acceptance rate than the NO-YES category.

5. A qualitative analysis of the papers on which SPCs and/or AC disagree with full review

As seen in Section 3, among the papers for which either the SPCs or
the AC wanted summary rejection, 9 have finally been accepted (1 in
category NO-YES, 4 in category YES-NO and 4 in category NO-NO). I
think it is interesting to say a few words on each of them, just to
illustrate the kind of situations in which SPCs and/or AC disagreed
with PCs. I thus read all the reviews and discussions of these 9
papers. We can separate these 9 papers in three main cases:

• (POSITIVE) The reviews are convincing enough (though often not very
  enthusiastic). The summary reject decision seems to have been too
  harsh,
• (NEUTRAL) The arguments from SPCs/AC and from PCs are incomparable
  or the paper is borderline,
• (NEGATIVE) The paper is clearly below the IJCAI standard.

Three papers can be classified as POSITIVE. Let us call them #A, #B,
and #C. #A is from the NO-YES category. #B and #C are from the YES-NO
category. #A only received 3 yes-votes among 7 SPC votes. The 4
no-votes all pointed out the lack of novelty but the AC saved #A
because it addresses an important application problem. The PCs liked
the good results on an important application domain and gave strong
accept, accept, and two weak accept in the full-review phase. #B and
#C both only received 2 no-votes (among 10 SPC votes for #B and among
7 for #C) and were summary rejected by the AC. For #B, the AC pointed
out the lack of evaluation of the contribution but this reason was not
even mentioned by the four PCs, who gave one accept and three weak
accept. #C was summary rejected by the AC without any comment. It was
also given one accept and three weak accept by the PCs, though very
lukewarm tone for all of them.

Four papers, let us call them #D, #E, #F, and #G can be considered as
NEUTRAL. They are all from the category NO-NO, which means that SPCs
and AC agreed that they are bad papers. #D and #E are clearly
borderline. The SPC of the full review phase (bear in mind this SPC is
not one of the SPC-voters) has been a bit too generous. PCs indeed
agreed that #D is technically weak and that #E lacks novelty. For #F
and #G, the SPCs/AC arguments and the PCs arguments are incomparable.
SPC-voters questioned the relevance of #F to IJCAI whereas the PCs
evaluated it as a strong, though extremely narrow, contribution. I saw
that #F does not cite any paper from IJCAI/AAAI/AIJ or any other major
conference in AI, which tends to concur with SPC votes. As for #G,
the SPCs/AC summary rejected it, following my recommendation, because
it was one of these papers that had clearly cheated on the keywords to
avoid reviewers specialists of the topic. PCs did not consider this.

Finally, the two remaining papers, #H and #J, can be classified as
NEGATIVE. They are YES-NO papers (4 yes-votes among 7 for #H and 6
yes-votes among 10 for #J). The PCs of #H seem to have accepted it
for the reason that it is clearly written despite they all agree it
has weak evaluation. #J was rejected by the AC because not motivated
and poorly organized. The SPC and AC of the full-review phase accepted
it despite its PCs all agree that it is badly written, too dense, not
clear, and of limited interest. Hence, it seems that we cannot
consider these two papers as misclassified by AC.

6. Conclusion on the impact of SPCs and ACs on summary-reject decisions

6.1 When SPCs and AC agree

When SPCs and AC agreed to send to full review (YES-YES papers), we
observe an acceptance rate of 23.8%, significantly higher than the
12.5% acceptance rate on all the 4734 papers in our analysis. Thanks
to the lottery winners we observe that when SPCs and AC agreed to
summary reject (NO-NO papers in lottery), the acceptance rate drops to
6.9%. Interestingly, none of the papers in these 6.9% are from the
POSITIVE subset. It thus seems that when SPCs and AC agreed to summary
reject a paper, the full-review phase did not show evidence that it
was a wrong decision.

6.2. When SPCs and AC disagree

Among the papers that the AC sent to full review despite the SPCs
wanted to summary reject, only one was finally accepted, giving a very
low 4.2% acceptance rate, even if that paper was a good one according
to the reviews (POSITIVE category in Section 5). For the papers that
the SPCs wanted to send to full review and the AC wanted to summary
reject, the acceptance rate in the lottery winners is 9.5%,
significantly higher than the 4.2% above. The best lottery winners
according to the reviews are in this category (POSITIVE). This tends
to show that the real misclassifications come more often from the ACs.

6.3. What if ACs were not involved in the summary-reject phase?

We can wonder what would have happened without the AC involved in the
summary-reject phase. If the summary-reject phase had automatically
rejected exactly those papers that SPCs wanted to summary reject, that
is, those papers with the ratio of yes-votes strictly smaller than
0.5, 1067 more papers would have gone for full review (excluding the
lottery winners) . This would have incurred a significantly higher
reviewing load, thus a drop in the quality of the assignment of papers
to PCs.

If we want SPC votes to lead to a similar reviewing load as what we
obtained with AC deciding summary reject (i.e., 2466 papers, excluding
the 100 lottery winners), the threshold above which the ratio of
yes-votes leads to full review has to be set to a value greater than
0.5. By setting the threshold to 0.66, 2592 papers go for full
review. Higher thresholds lead to less than 2466 papers sent to full
review. If we had sent these 2592 papers to full review instead of the
2466 we sent, would the results be better or worse in terms of
misclassified papers? 12 of the lottery winners would have
automatically been sent to full review. Among these 12, 2 belong to
the accepted lottery winners, which makes a 16.67% acceptance rate for
these extra papers that SPCs would send to full review and that ACs
had summary rejected. Interestingly, these 2 papers are the two papers
that received the best reviews among the 8 accepted lottery
winners. The counterpart is that 153 papers that the AC had decided to
send to full review would now be summary rejected. Among these 153
papers, 18 were eventually accepted at the full review phase, which
makes a 11.8% acceptance rate for those papers that SPCs would reject
pursuant to this new policy. Compared to the 16.67% acceptance rate
for the papers that SPCs would send to full review, this gives an
advantage to the policy consisting in using only SPC votes to decide
which paper goes to full review. Another obvious advantage of this
policy in which ACs are discarded from the summary reject phase is to
release them from this duty.

7. Summary and additional observations

In addition to the detailed analysis contained in the former sections,
here are a few general pros and cons that I draw from this experience.

PROS:

• The summary-reject phase often gave a valuable, though different,
  point of view on the papers compared to what reviews contain.
• The fact that 7 to 10 SPCs were asked to vote on a same paper has
  been very robust to unresponsive SPCs. Even if one or two SPCs did
  not respond, the AC still had enough votes to take a decision. This
  was particularly appreciated given the tight schedule in which this
  phase had to fit.
• A statistical analysis has shown that the ratio of SPCs yes-votes
  was well correlated to the chances to be accepted after full review.
• There is another good feature of this voting process that could be
  useful although I have not used it. If we are able to predict in
  advance the maximum number of papers the set of PCs are able to
  handle with good quality paper matching, we can adjust the threshold
  of yes-votes that allows a paper to go to full review so that the
  number of papers sent to full review is close to that maximum.

CONS:

• SPCs have seen the summary-reject phase as an extra-load on their
  shoulders despite the fact they no longer had papers to review
  during full-review phase. I explain this by a reluctance to
  new/unknown duties.
• Following the analysis reported in Section 6, it seems that a more
  accurate summary-reject policy would have been possible by using SPC
  votes alone to decide summary-reject.
• The major drawback of the way I implemented the summary-reject
  procedure is that authors had difficulties to accept a
  summary-reject decision not justified by any review.

8. Final comment

The summary-reject phase has been introduced to tackle the issue of
receiving more submissions than what the program committee can
handle. But we should bear in mind that the exponential increase in
number of submissions mainly affects machine learning, vision, and
natural language processing. If the IJCAI community was ready to
accept that papers are processed differently depending on the area,
the summary-reject phase could be limited to those three critical
areas for which the number of submissions exceeds what can be reviewed
with the expected quality standard. I didn't choose that option, but
the question deserves to be raised.

Many of us think that the increase in number of IJCAI submissions in
machine learning, vision and natural language processing is correlated
with a decrease of the quality of papers submitted to IJCAI in those
areas. Hence, if we don't consider the equity issue, it would make
sense to apply a review process that depends on the area.

Though I am not able to assess whether the level of quality of the
papers submitted to IJCAI in machine learning, vision, and natural
language processing has decreased, I can use the statistics from 2020
to see whether, in the eyes of the PCs, those papers have the same
level of quality as in other areas or not.

Let us separate areas in two categories: The category including
machine learning, vision, and natural language processing --let us
call it 'popular areas', and the category 'other IJCAI areas'. I
discarded the areas 'multidisciplinary topics and application' and
'humans and AI' from this analysis because it is not obvious which
category they should be assigned to.

A first observation is that the ratio of summary-rejected papers in
other IJCAI areas is significantly lower than in the popular areas:
28.3% against 48.9%. We could think that it is due to behavior of SPCs
which is more selective in the popular areas than in the other IJCAI
areas. If so, either popular areas should have a higher acceptance
rate at the full review phase --in the case SPCs have the same
criteria as PCs in full review-- or the summary-reject phase should
show a higher rate of misclassified papers --in the case SPCs used
different criteria or were too harsh.

Do popular areas have a higher acceptance rate at the full review
phase? No. We observe that despite the looser summary-reject selection
for other IJCAI areas, their acceptance rate in the full review phase
is higher than that of the popular areas: 27.6% against 21.4%. Do
popular areas suffer from more misclassified papers? No. Among the 8
misclassified papers in the lottery winners set, 4 among 44 belong to
other IJCAI areas and 3 among 43 belong to popular areas. It thus
seems that the summary-reject phase didn't lead to more
misclassifications in popular areas than in other IJCAI areas. All
this tends to show that the summary-reject phase was not too selective
in popular areas. According to the PCs, the difference with other
IJCAI areas seems to come from the lower quality of the submissions.