


Next: Sous projet Langages
Up: Sous projet: Sémantique
Previous: Réorganisation de hiérarchies
Responsable: Michel Habib
Chercheurs impliqués: Michel Habib, Marianne Huchard,
Lhouari Nourine - LIRMM
Thème et objectif scientifiques:
Dans de nombreuses applications, il est important de pouvoir stocker
et manipuler efficacement les hiérarchies d'héritage qui sont des graphes sans
circuit ou des treillis. Ce problème est un cas particulier de celui
du codage d'un ordre.
Un codage ou plongement d'un ordre est une application f d'un ordre
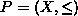 dans un ordre
dans un ordre 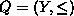 telle que
telle que 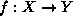 et vérifie:
et vérifie: 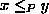 si et seulement si
si et seulement si 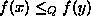 . Un tel codage
est intéressant lorsque la relation d'ordre sur Q est plus facile
à manipuler que celle sur P, où lorsque la place mémoire
utilisée est réduite.
L'opération couramment utilisée est du type test de comparabilité
. Un tel codage
est intéressant lorsque la relation d'ordre sur Q est plus facile
à manipuler que celle sur P, où lorsque la place mémoire
utilisée est réduite.
L'opération couramment utilisée est du type test de comparabilité 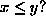 ,
mais dans le cas des treillis, il est naturel de vouloir calculer efficacement
des bornes supérieures ou inférieures.
,
mais dans le cas des treillis, il est naturel de vouloir calculer efficacement
des bornes supérieures ou inférieures.
Les codages les plus fréquents sont ceux où Q est un treillis
booléen, on obtient alors des codages par vecteurs de bits.
Les problèmes d'optimisation sous-jacents sont NP-difficiles et la
détermination de l'optimum semble être un problème combinatoire
extrêmement difficile, mais
aucun argument théorique n'interdit
de construire des codages optimaux sur des classes particulières
d'ordres ou de concevoir des heuristiques très efficaces pour le cas
général.
Les principales heuristiques actuelles ont été proposées par
Aït-Kaci, Caseau, Ellis et Habib-Huchard-Nourine.
L'objectif est de produire des codages plus efficaces que ceux
actuellement proposés, tout en restant calculables efficacement.
Un deuxième problème voisin est celui de l'organisation (indexation)
de bases de données de graphes (par exemple de graphes de molécules)
qui permette la recherche efficace d'appariements.
Par exemple si l'on veut rechercher à partir d'une molécule donnée
toutes les molécules de la base qui sont contenues (morphisme
injectif) dans la molécule donnée.
Etat d'avancement: Nous avons formalisé dans [HHN95] ce
problème de codage comme
celui du calcul d'une nouvelle dimension dite dimension de
codage, qui est le plongement le plus efficace d'un ordre dans un
produit de chaînes. Nous avons montré que la 2-dimension ou dimension
booléenne (plongement dans un produit de chaînes à 2
éléments) était une bonne approximation. En outre nous avons
proposé une heuristique de codage basée sur une décomposition
coatomique des treillis.
Dans [HN95] nous avons proposé une autre heuristique de calcul
de la 2-dimension basée sur un théorème de décomposition.
Relations nationales et internationales:
Nous sommes en liaison étroite avec les principaux chercheurs du
domaine (Aït-Kaci et son étudiant A. Fall de Vancouver (Canada),
G. Ellis de Melbourne (Australie), Y. Caseau de l'ENS).



Next: Sous projet Langages
Up: Sous projet: Sémantique
Previous: Réorganisation de hiérarchies
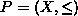 dans un ordre
dans un ordre 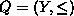 telle que
telle que 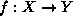 et vérifie:
et vérifie: 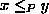 si et seulement si
si et seulement si 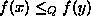 . Un tel codage
est intéressant lorsque la relation d'ordre sur Q est plus facile
à manipuler que celle sur P, où lorsque la place mémoire
utilisée est réduite.
L'opération couramment utilisée est du type test de comparabilité
. Un tel codage
est intéressant lorsque la relation d'ordre sur Q est plus facile
à manipuler que celle sur P, où lorsque la place mémoire
utilisée est réduite.
L'opération couramment utilisée est du type test de comparabilité 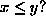 ,
mais dans le cas des treillis, il est naturel de vouloir calculer efficacement
des bornes supérieures ou inférieures.
,
mais dans le cas des treillis, il est naturel de vouloir calculer efficacement
des bornes supérieures ou inférieures.