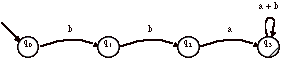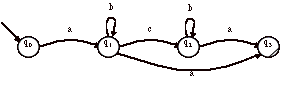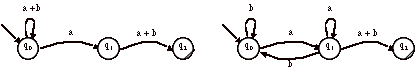Chapitre 2

Automates d’états finis
et langages réguliers

2.1 Automates d'états finis

Définition informelle

Notations

Reconnaissance d'un mot

Définition formelle des automates finis déterministes

Automates finis non-déterministe

Automates avec e-transition

Équivalences d'automates

2.2 Transformation d'une expression régulière en un automate

Propriété

Cas de base

Récurrence

. Élimination des e-transitions

2.3 Transformation d'un automate en une expression régulière

Par réduction d'automates

Par résolution d'équations

2.4 Déterminisation et Minimisation

Méthode de déterminisation

Relation d'équivalence sur les langages réguliers

2.5 Autres opérations sur les automates

Automate complémentaire

Automate miroir

Intersection de deux automates

2.6 Conclusion

Dans ce chapitre, nous présentons et étudions la classe de machines abstraites que sont les automates à états finis réguliers. Ces automates sont strictement équivalents en puissance aux langages réguliers. Ils constituent le niveau le plus faible des machines et langages qui nous étudierons.

Après avoir présenté les différentes variations possibles sur les automates réguliers, nous abordons, en détail, la transformation d’une expression régulière vers un automate. Elle est présentée selon deux approches distinctes quoique strictement équivalentes : la réduction d’automates et la résolution d’équations. Certains problèmes sur les expressions régulières peuvent être aisément résolus en passant par les automates les reconnaissant. De façon similaire, nous présentons ensuite la transformation inverse, d’un automate en une expression régulière.

La « déterminisation » permet de passer d’un automate non-déterministe, souvent facile à trouver, à son équivalent déterministe. Cette transformation se base sur la définition d’une relation d’équivalence sur les états.

Enfin, plusieurs opérations sur les automates sont introduites : intersection, complémentaire, image miroir. Ces opérations sont en général faciles sur les automates mais difficiles à réaliser sur les expressions régulières.

1. Automates d’états finis

1.1. Définition informelle

Un automate effectue un ensemble d’actions et fournit un résultat. En ce sens un s’agit d’un algorithme. L’objet de cette classe d’algorithmes est de reconnaître si un mot donné appartient à un langage régulier que décrit l’automate.

L’automate d’états finis (déterministe ou non) est composé de :

· Une bande (infinie) de lecture comportant des cases. Chaque case contient un caractère de V ;

· Une tête de lecture désignant une case particulière ;

· Un dispositif de contrôle pouvant prendre un nombre finis d’états. Ce dispositif peut être dans l’état 0, 1, 2, 3, …

· L’automate dispose d’une table de transition (son programme). Cette table de transition précise le changement d’état de l’automate :

	a	b	c	…	s	…
® 0	1	-	2
¬ 1	-	1
2	1	2
…
q					q’
…

L’automate étant dans l’état q. Sa tête de lecture désigne une case contenant le symbole s. Alors :

· L’automate passe dans l’état q’ ;

· Sa tête de lecture se déplace sur la case suivante (celle située immédiatement à droite de la case de s).

Parmi l’ensemble des états de l’automate, on distingue les états initiaux (états d’entrée) et les états finals (états de sortie). Un état initial peut aussi être final. En général, on s’ « arrange » pour n’avoir qu’un seul état initial.

On note L(A) l’ensemble des mots reconnus par l’automate A. Pour les automates d’états finis , cet ensemble est un langage régulier.

1.2. Notations

Une notation graphique équivalente à la notation tabulaire est proposée. Dans le reste de ce cours on tendra à privilégier la notation graphique plus immédiatement lisible. Toutefois, il est parfois nécessaire de passer de l’une à l’autre.

La notation tabulaire est celle utilisée par les algorithmes de construction et de transformation d’automates.

> Par exemple, les deux représentations ci-dessous sont équivalentes :

	a	b	c
® 0	1	-	2
¬ 1	-	1	-
2	1	2	-

<

Sous la forme tabulaire, on indique par une flêche entrante (®) les états initiaux. On indique par une flêche sortante (¬) les état finaux. Les transitions inexistantes laissent des cases vides (-).

Sous la forme graphique, on indique les états initiaux à l’aide d’une flêche sans origine. Les états finaux sont barrés.

Une notation fonctionelle est aussi parfois utilisée. Celle-ci est proche de la définition formelle. Elle introduit une fonction de transition : d(un état, un élément de V) = un état.

> Pour l’automate ci-dessus, on a la notation fonctionnelle suivante :

V = {a, b ,c}

états = {0, 1, 2} états initiaux = {0} états finals = {1}

d(0, a) = 1, d(0, c) = 2, d(1, b) = 1, d(2, a) = 1, d(2, b) = 1

<

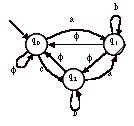
On remarquera qu’une transition inexistante est équivalente à une transition f, et que l’automate précédent pourrait être (beaucoup plus lourdement) écrit :

>

	a	b	c
® 0	1	f	2
¬ 1	f	1	f
2	1	2	f

<

Un automate est dit « bien formé » s’il vérifie les conditions suivantes :

· il n’existe aucune transition portant f ;

· tous les états sont ateignables à partir d’un état initial.

Sauf indication contraire on ne considèrera que des automates bien formés.

Un automate est dit « saturé » s’il vérifie les conditions suivantes :

· il n’existe aucune transition portant f ;

· de chaque état partent au moins une transition pour chaque élément de V.

1.3. Reconnaissance d’un mot

Un mot est reconnu par l’automate si, à partir de la position initiale (automate dans l’état initial, et la tête de lecture désignant le premier caractère de ce mot), l’automate parcours le mot en entier et termine son parcours dans un état final.

> Par exemple, soit l’automate suivant :

	a	b	c
® 0	1	-	-
1	2	1	3
¬ 2	-	-	-
3	2	3

Sans le démontrer formellement, nous pouvons « deviner » que cet automate reconnaît le langage décrit par l’expression régulière :

ab*(a + cb*a)

Faisons fonctionner l’automate sur le mot « abba »

1)

a

b

b

a

2)

a

b

b

a

3)

a

b

b

a

4)

a

b

b

a

5)

a

b

b

a

L’automate a parcouru complètement le mot et il s’arrête dans l’état final q₂. Le mot est donc reconnu.

Essayons pour le mot « abab » :

1)

a

b

a

b

2)

a

b

a

b

3)

a

b

a

b

4)

a

b

a

b

La transition (q₂, b) n’est pas définie. L’automate s’arrête sans avoir parcouru le mot. Le mot n’est donc pas reconnu.

Essayons pour le mot « abc» :

1)

a

b

c

2)

a

b

c

3)

a

b

c

4)

a

b

c

L’automate a parcouru complètement le mot, il s’arrête donc dans l’état q₃ qui n’est pas un état final. Le mot n’est donc pas reconnu.

<

Nous avons deux cas où l’automate refuse un mot (c’est-à-dire que le mot n’appartient pas au langage reconnu par l’automate) :

· soit, avant d’avoir parcouru complètement le mot, l’automate se trouve bloqué dans un état non final ;

· soit, après avoir parcouru complètement le mot, l’automate ne se trouve pas dans un état final.

1.4. Définition formelle des automates finis déterministes (AFD)

Un automate d’état fini déterministe est un quintuplet :

A_det= (V_T, Q, Q₀, F, m)

où

Q est un ensemble fini d’états ;

Q₀ Î Q ;

F Ì Q ;

V_T est un ensemble fini de symboles – le vocabulaire ;

m est une fonction de transition : Q ´ V_T ® Q ;

La fonction de transition induit une relation binaire (notée a) sur l’ensemble Q ´ V_T* de la manière suivante :

(q, sw) a (q’, w) Û m(q, s) = q’

Soit a* l’extension réflexive et transitive de la relation a.

" q Î Q, w Î V* (q, w) a* (q, w)

" q, q’, q’’ Î Q, w, w’, w’’ Î V*

(q, w) a (q’, w’) Ù (q’, w’) a* (q’’, w’’) Þ (q, w) a* (q’’, w’’)

Alors w Î L(A) si et seulement si :

$ q Î F : (q₀, w) a* (q, e)

Le mot w appartient au langage reconnu par l’automate si il existe un chemin de l’état initial à un état final qui décrit ce mot.

e Î L(A) Û q₀ Î F

e est un mot du langage reconnu par l’automate si l’état initial est final.

1.5. Définition formelle des automates finis non déterministes (AFN)

Pour un automate d’état fini non déterministe, la fonction de transition est définie sur des ensembles. On a donc :

A_ndet= (V_T, Q, Q₀, F, m’)

où

Q est un ensemble fini d’états ;

Q₀ Î Q ;

F Ì Q ;

V_T est un ensemble fini de symboles – le vocabulaire ;

m’ est une fonction de transition : Q ´ V_T ® Ã(Q) ; Ã(Q) représente les parties de Q.

La relation de transition devient :

(q, sw) a (q’, w) Û q’ Î m(q, s)

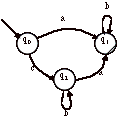
> Par exemple, soit l’automate non-déterministe suivant :

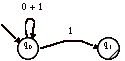
	0	1
® 0	0	0, 1
¬ 1	-	-

Cet automate permet la reconnaissance des mots sur V_T = {0, 1} se terminant par 1.

Faisons fonctionner l’automate sur le mot « 01 »

1)

0

1

2)

0

1

3) À ce stade, nous avons, le choix entre deux possibilités, choisissons la transition vers q₀.

0

1

Ce fonctionnement rejète le mot.

Réessayons, en choisissant l’autre chemin.

1’)

0

1

2’)

0

1

3’) Choisissons la transition vers q₁.

0

1

Ce fonctionnement accepte le mot.

Nous avons mis en évidence une façon d’accepter le mot. Le mot appartient donc à L(A).

<

On remarquera qu’il est souvent plus facile de trouver un automate non-déterministe que déterministe. Nous verrons dans la suite qu’il est possible de « déterminiser » un automate.

4 Construisez l’automate du langage L sur V={a, b} ne contenant que les mots qui se termine par « abb ».

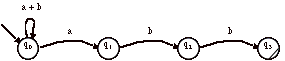Réponses : L’automate non-déterministe est très simple.

L’expression régulière est également simple :(a+b)*abb. Comment peut-on procéder pour la « deviner » ?

Essayez de construire une version déterministe de l’automate. Que constatez-vous ?

3

On remarquera qu’un automate non-déterministe est souvent plus petit que sa version déterministe. Cependant, son exécution est plus complexe. Il faut en effet se remémorer chaque point de choix et y revenir un cas d’échec.

1.6. Automate avec e-transition

Un automate avec e-transition (eAEF) dispose d’une fonction de transition définie sur V_T È {e}. La relation de transition devient donc :

(q, w) a (q’, w) Û q’ Î m(q, e)

(q, sw) a (q’, w) Û q’ Î m(q, s)

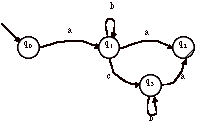
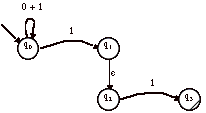
> Par exemple, soit l’automate suivant :

	e	0	1
® 0	-	0, 1	0
1	2	-	-
2	-	-	3
¬ 3	-	-	-

Faisons fonctionner cet automate sur « 01 »

1)

0

1

2)

0

1

3) On prend la e-transition qui ne fait pas avancer la tête de lecture sur la bande.

0

1

4)

0

1

Ce fonctionnement accepte le mot.

<

1.7. Équivalences d’automates

La classe des automates d’états finis (AEF) est la plus générale. Les automates finis peuvent être déterministes (AEF-det) ou non déterministe (AEF-ndet). De plus, ils peuvent (ou non) contenir des e-transitions (de façon générale, nous appellerons ce type d’automate des e-automates). Les e-automates sont non-déterministes.

On verra que tous ces types d’automates sont rigoureusement identiques et que l’on peut toujours se ramener, par simplification et « déterminisation » à un AEF-det.

Pour résumer, un automate est considéré comme non-déterministe (au sens large) si au moins une des conditions suivantes est vérifiée :

· Il existe au moins plusieurs transitions t₁, t₂, … t_n portant le même symbole x partant d’un état unique q vers plusieurs états q₁, q₂, … q_n ;

· Il existe au moins une e-transition ;

· Il existe plus d’un état initial.

Autrement dit, s’il existe à un moment donné un point de choix lors de la reconnaissance d’un mot, l’automate n’est pas déterministe. De plus, à chaque étape, le pointeur doit avancer sur la bande de lecture.

4 pour un mot de longueur l appartenant à L(A), A étant déterministe, combien d’étapes sera-t-il nécessaire pour que l’automate le reconnaisse ?

Que peut-on dire pour un mot qui n’appartient pas à L ?

Que peut-on dire si l’automate est saturé ? Que peut-on dire si l’automate n’est pas bien formé ?

3

On remarquera, par ailleurs, que pour tout automate A, on peut créer un automate A’, n’ayant qu’un seul état initial et qu’un seul état final, tel que L(A) = L(A’).

En effet, si on a plusieurs états finals, il suffit de créer un nouvel état final F et de relier à l’aide de e-transitions les états finals d’origine à cet état F.

De façon analogue, si on a plusieurs états initiaux, il suffit de créer un nouvel état initial I et de relier à l’aide de e-transitions cet état I aux états initiaux d’origine.

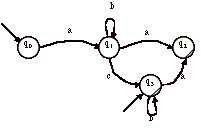
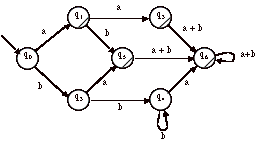
> Par exemple, soit l’automate A suivant :

	a	b	c
® 0	1	-	-
1	2	1	3
¬ 2	-	-	-
® ¬ 3	2	3

On peut « deviner » que le langage reconnu par cet automate pourrait être noté par l’expression régulière :

ab*a + ab*cb* + ab*cb*a + b* + b*a

= ab*a + ab*cb*(e + a) + b*(e + a)

= ab*a + (ab*c + e)b*(e + a)

L’automate ayant une structure simple, il est possible de suivre (sans en oublier) les différents chemins. Une telle méthode n’est pas toujours aisée si l’automate est plus touffu.

1) Soit A’ l’automate obtenu par ajout d’un état final unique :

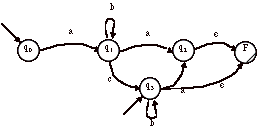
	e	a	b	c
® 0		1	-	-
1		2	1	3
2	F	-	-	-
® 3	F	2	3
¬ F	-	-	-

2) Soit A’’, l’automate obtenu par ajout d’un état initial unique :

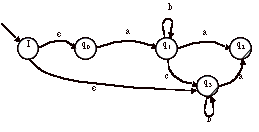
	e	a	b	c
® I	0, 3	-	-	-
0		1	-	-
1		2	1	3
¬ 2		-	-	-
¬ 3		2	3

3) On obtient donc l’automate A’’’ par combinaisons de A’ et A’’ :

	e	a	b	c
® I	0, 3	-	-	-
0		1	-	-
1		2	1	3
2	F	-	-	-
3	F	2	3
¬ F

L’automate ainsi obtenu peut éventuellement être simplifié.

Il n’y a aucune transition entrante dans l’état initial et aucune transition sortante de l’état final. <

4 Exercice : vérifier qu’à chaque étape le langage reconnu par l’automate reste inchangé.

3

Dans le cas d’un automate disposant d’un état initial et d’un état final unique, il est parfois pratique de simplifier la notation graphique. Cette nouvelle notation permet de « masquer » les détails liés à l’automate pour ne se concentrer que sur son entrée et sa sortie.

Avec L(A) = L(R), un automate A peut se noter comme suit :

> À partir de l’exemple précédent, on pourra donc avoir :

<

2. Transformation d’une expression régulière en un automate

2.1. Propriété

Soit la propriété S(n) définie comme suit :

Si R est une expression régulière à n occurrences d’opérateurs et aucune variable comme opérandes atomique (.) alors il existe un e-automate A qui accepte les mots de L(R) et aucune autres. A n’a :

· Qu’un seul état d’acceptation (état final) ;

· Pas d’arc vers son état initial ;

· Pas d’arc issu de son état final.

2.2. Cas de base

Soit la case de base S(0) défini comme suit :

Si n=0 alors R doit être un opérande atomique qui est : soit f, soit e, soit x pour un certain symbole x (x Î V). Pour chacun des trois cas, on peut concevoir un automate à 2 états pour lequel S(0) est vrai :

2.2. Récurrence

Nous allons supposer que si on a S(n) alors nous avons S(n+1) :

Nous allons créer de nouveaux automates. Pour chaque occurrence de l’expression régulière, on crée un état particulier.

> Par exemple, si l’expression régulière contient 3 a, alors on créera 6 états sur le modèle :

<

Supposons que S(i) soit vraie pour tout i supérieur ou égal à n ("i £ n). Autrement dit, pour une expression régulière R quelconque avec au plus n occurrences d’opérateurs, il existe un automate satisfaisant à l’hypothèse de récurrence et acceptant tous les mots de L(R) et seulement ceux-là.

Soit R une expression régulière avec (n+1) occurrences d’opérateurs.

On s’intéresse à l’opérateur le plus extérieur, c’est-à-dire, la racine de la structure syntaxique. Alors R est de la forme R₁ + R₂, ou R₁.R₂ ou R₁*

Dans chacun des trois cas, R₁ et R₂ ne peuvent comporter plus de n occurrences car l’opérateur situé à la racine de la structure syntaxique ne fait partie ni de R₁ ni de R₂, et que R a exactement (n+1) occurrences d’opérateurs.

L’hypothèse de récurrence s’applique donc à R₁ et R₂ dans chacun des trois cas. On peut alors démontrer S(n+1) dans chacun des trois cas.

On remarquera, par ailleurs, que pour tout automate A, on peut créer un automate A’, n’ayant qu’un seul état initial et qu’un seul état final, tel que L(A) = L(A’).

En effet, si on a plusieurs états finals, il suffit de créer un nouvel état final F et de relier à l’aide de e-transitions les états finals d’origine à cet état F.

De façon analogue, si on a plusieurs états initiaux, il suffit de créer un nouvel état initial I et de relier à l’aide de e-transitions cet état I aux états initiaux d’origine.

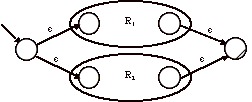1) R = R₁ + R₂

L’état initial associé à R comporte des e-transitions vers les états initiaux des automates associés à R₁ et R₂. Les anciens états initiaux deviennent des états ordinaires.

Les états finals (d’acceptation) de ces deux automates deviennent des états ordinaires et on ajoute des e-transitions vers l’état d’acceptation du nouvel automate.

La seule façon d’atteindre l’état final à partir de l’état de départ consiste à suivre un arc étiqueté e dirigé vers R₁ (resp. vers R₂) puis de reconnaître un mot de L(R₁) (resp. de L(R₂)) et à partir de l’état d’acceptation de R₁ (resp. R₂) d’effectuer la e-transition vers l’état d’acceptation de L(R₁) È L(R₂) c’est-à-dire L(R).

2) R = R₁ . R₂

L’état final de R₁ et l’état initial de R₂ deviennent des états ordinaires. L’état initial de R₁ devient l’état initial de R et l’état final de R₂ devient l’état final de R.

La seule façon de passer de l’état à l’état final est de lire un mot de R₁ puis de lire un mot de R₂.

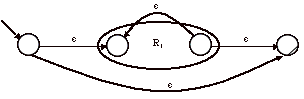3) R = R₁* = e + R₁⁺

La répétition non nulle (+) consiste à relier l’état final de l’automate de R à son état initial. Pour ajouter e au langage reconnu par l’automate, il suffit de créer un nouvel état initial et un nouvel état final et de les relier avec une transition e.

Pour passer de l’état initial à l’état final, on passe soit par la transition directe e (et le mot e est reconnu), soit on passe par une reconnaissance du L(R₁) puis une transition directe. Lorsque l’on a reconnu un mot de L(R₁), il est possible de recommencer un nombre quelconque de fois en utilisant la e-transition entre l’état final et l’état initial de R₁.

4 Expliquer pourquoi pour rajouter e au langage reconnu par un automate A, il n’est pas possible dans le cas général de rendre l’état initial de A final.

Donner un exemple. Exhiber un cas particulier où l’on pourrait procéder de la sorte.

3

Donc d’après 1), 2) et 3) nous avons vérifié S (n+1).

et donc S(n) est vraie pour tout n.

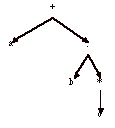> Considérons par exemple l’expression régulière : a + bc*

La structure syntaxique est :

Soient pour chacun des atomes « a », « b » et « c », les automates suivants :

Automate pour c* :

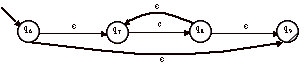
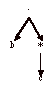Automate pour bc* :

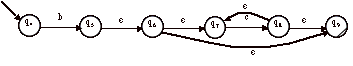
Automate pour a+ bc* :

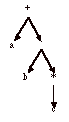
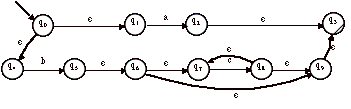
Il est possible (et même recommandé) de simplifier cet automate.

<

4 Essayer de trouver l’expression régulière à l’automate ci-dessus. Comment peut-on décomposer les chemins de l’automate ?

Réponses : On peut essayer de lire les chemins de l’automate. L’absence de boucle trop compliquée doit rendre cette lecture possible.

Nous avons les chemins suivants avec leur expression régulière associée :

<q0, q1, q2, q3> º e.a.e º a

<q0, q4, q5, q9, q3> º e.b.e.e.e º b

<q0, q4, q5, q6, q7, q8, q9, q3> º e.b.e.e.c.(e.c)*.e.e º b.cc*

L’expression régulière de l’automate est l’union des expressions régulières ci-dessus : a + b + bcc* = a + bc*

3

2.4. Élimination des e-transitions

Dans un automate, si l’on se trouve dans un état q quelconque comportant des e-transitions, on se trouve en réalité dans le même temps dans chaque état accessible q’ à partir de q en suivant les e-transitions.

En effet, soit le w le mot étiquetant le chemin de q₀ (état initial) à q, alors w. e (= w) est le chemin étiquetant le chemin de q₀ à q’.

L’élimination des e-transitions est effectuée en quatre étapes :

1. Augmentation des transitions ;

2. Propagation des états finals ;

3. Suppression des e-transitions ;

4. Élimination des états inaccessibles.

On construit un nouvel automate où il existe une transition entre l’état qi et l’état q_j étiqueté par x s’il existe un état q_k tel qu’il existe une suite d’e-transitions que q_i à q_k et qu’il existe une transition x de q_k à q_j.

> Si on augmente les transitions à partir de l’automate donné en exemple ci-dessus, on obtient le nouvel automate suivant :

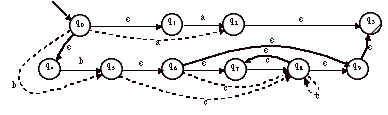
Un état est final s’il existe une suite d’e-transitions qui mène à un état final.

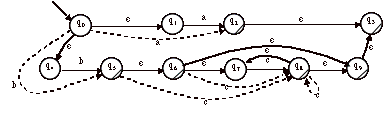
On supprime les e-transitions.

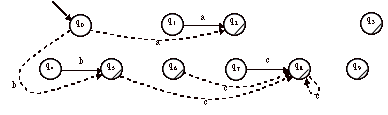
On supprime les états inaccessibles à partir de l’état initial.

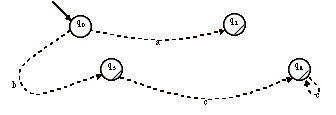
On obtient comme résultat final l’automate défini à partir de l’expression régulière = a + bc*. <

3. Transformation d’un automate en une expression régulière

3.1. Par réduction d’automates

Dans la méthode par réduction d’automates, la construction de l’expression régulière définissant le même langage que celui reconnu par l’automate passe par la suppression successive des états de l’automate A.

Pour ce faire, on remplace successivement l’étiquetage des transitions de l’automate par des expression régulières.

On considère l’étiquette d’un chemin comme la concaténation des expressions régulières associées à ce chemin.

> Par exemple :

<

Soit un automate déterministe A. Considérons un état q non-final à n états prédécesseurs (pi) et n états successeur (si) et éventuellement une transition sur lui-même. Cet état q peut-être éliminé à condition de « mettre à jour » les transitions restantes de l’automate

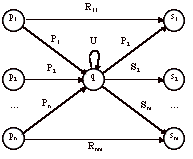
Chaque transition est définie par une expression régulière. L’élimination de q doit donc modifier les transitions p_i à s_j (pour tout 1£i£ n et 1£j£m).

La transition allant de p_i à s_j sera modifiée de façon à porter l’expression régulière : R_ij + P_iU*S_j

En effet, si on passe de p_i à s_j directement cela s’effectue en acceptant un mot de l’expression régulière R_ij.

Si on passe par q, il faut :

Reconnaître un mot défini par P_i ;

Reconnaître 0 ou n fois un mot défini par U ;

Reconnaître un mot défini par S_i.

Donc au total, il faut reconnaître un mot de l’expression régulière P_iU*S_j.

La méthode consiste donc à éliminer tous les états sauf les états finals (et bien sûr l’état initial). Lorsque l’automate ne comprend qu’un état initial et un état final (éventuellement confondus), on peut en déduire le langage reconnu.

Le langage reconnu est : S*U(T + VS*U)*.

Si l’automate A ne comporte plus qu’un seul état initial et n (n>1) états finals (notés F_i), on crée n copies de l’automates. Pour chaque copie A_i, seul l’état F_i est final. L’expression régulière R(A) sera l’union des expressions R(A_i) : R(A) = R(A₁) + R(A₂) + R(A₃) + … R(A_n)

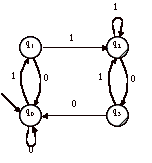> Soit par exemple, l’automate A suivant :

Essayons de trouver une expression régulière R(A) du langage L(A).

On souhaite éliminer l’état q₁. Les prédécesseurs de q₁ sont {q₀}. Les successeurs de q₁ sont {q₀, q₂}. Il n’y aucune boucle sur q₁, on considère donc qu’il y a une boucle étiquetée f.

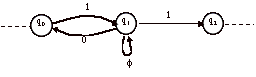
On supprime q₁ et on ajoute les transitions q₀-q₀ et q₀-q₂.

On obtient donc l’automate A’ suivant :

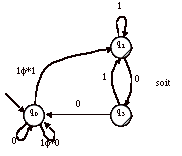
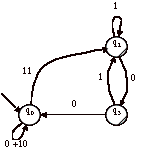
L’automate A’ contient deux états finals et un état initial. Il n’est pas possible continuer à éliminer directement des états, il est nécessaire de dupliquer A’.

Soient B et C, les deux copies de A’ :

	et

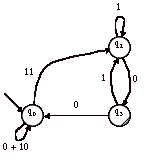
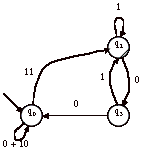
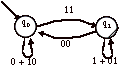Pour B, on élimine q₃ :

Le langage reconnu par B est : (0+10)*11(1+01+00(0+10)*11)*

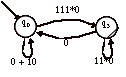Pour C, on élimine q₂ :

Le langage reconnu par C est : (0+10)*111*0(1*10+0(0+10)*111*0)*

Le langage reconnu par A est donc :

(0+10)*11(1+01+00(0+10)*11)*
+ (0+10)*111*0(1*10+0(0+10)*111*0)*

<

4 : essayer de monter que l’expression régulière R(A) ci-dessus décrit le langage L sur {0, 1} de tous les mots possibles ne se finissant pas par « 00 ».

Éléments de réponse :

Une expression régulière simple pour L est : (0+1)*01 + (0+1)*10 + (0+1)*11

On peut observer l’expression régulière R(A).

Avons-nous R(A) = R(L) ? Il y a plusieurs manières de procéder. Lesquelles ?

3

3.2. Par résolution d’équations

À partir d’un automate A, il est possible de poser les équations décrivant les langages reconnus par chaque état. C’est-à-dire que pour chaque état on se pose la question suivante « quel serait le langage reconnu en commençant par cet état ? ».

Pour n états, on trouvera donc, n équation à n inconnues. On note L(i), le langage reconnu à partir de l’état i. L’objectif est de résoudre l’équation pour la variable L(0). L(0) est le langage reconnu à partir de l’état initial, c’est-à-dire le langage reconnu par l’ensemble de l’automate donc L(A).

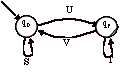Comme pour la méthode par réduction d’automates, le cas général minimal est :

Les équations associées sont :

L(0) = S . L(0) + U . L(f)

L(f) = T . L(f) + V . L(0) + e

On remarquera qu’un état final reconnaît au moins {e}, c’est-à-dire l’expression régulière e.

La résolution du système d’équation se fait comme en arithmétique par substitution et réécriture. De plus, quand on trouve une équation de la forme : L = xL + y alors sa solution est x*y.

L = xL + y Þ L = x*y

Résolvons le système d’équations ci-dessus :

a) L(0) = S . L(0) + U . L(f)

b) L(f) = T . L(f) + V . L(0) + e

on obtient par résolution

c) L(f) = T*(V . L(0) + e)

on remplaçant L(j) dans a)

d) L(0) = S . L(0) + UT*(V . L(0) + e)

L(0) = (S + UT*V) L(i) + UT*

L(0) = (S + UT*V)*UT*

Nous avons L(0) = S*(UT*VS*)*UT*

car (x + y)* = x*(yx*)* et ici x = S et y = UT*V

L(0) = S*U(T*VS*U)*T*

car (xy)*x = x(yx)* et ici x = U et y= T*VS*

L(0) = S*U(VS*U + T)*

car (x*y)*x* = (x + y)*et ici x = T et y = VS*U

L(0) = S*U(T + VS*U)*

Donc nous avons : (S + UT*V)*UT* = S*U(T + VS*U)*. C’est-à-dire que dans le cas général minimal on obtient un résultat équivalent à celui par la méthode de réduction d’automate.

4 démontrez que la méthode par résolution d’équation est équivalente à celle de réduction d’automates.

Éléments de réponse : il est possible de procéder par induction. La suppression d’un état équivaut à la substitution de la variable associée dans le système d’équations. Quel est le cas de base ?

3

> Par exemple, soit l’automate A suivant :

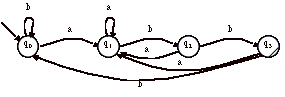
Cet automate est l’automate déterministe reconnaissant les mots de la forme :(a+ b)*abb. Essayons de retrouver l’expression régulière.

On pose les équations suivantes :

a) L(0) = bL(0) + aL(1)

b) L(1) = aL(1) + bL(2)

c) L(2) = aL(1) + bL(3)

d) L(3) = bL(0) + aL(1) + e

On peut dans c) remplacer L(3) par sa définition

e) L(2) = aL(1) + b(bL(0) + aL(1) + e)

L(2) = aL(1) + bbL(0) + baL(1) + b

On peut dans b) remplacer L(2) par sa définition

f) L(1) = aL(1) + b(aL(1) + bbL(0) + baL(1) + b)

L(1) = aL(1) + baL(1) + bbbL(0) + bbaL(1) + bb

L(1) = (a + ba + bba)L(1) + bbbL(0) + bb

L(1) = (a + ba + bba)*(bbbL(0) + bb)

On peut remplacer dans a) remplacer L(1)

g) L(0) = bL(0) + a(a + ba + bba)*(bbbL(0) + bb)

L(0) = bL(0) + a(a + ba + bba)*bbbL(0) + a(a + ba + bba)*bb

L(0) = (b + a(a + ba + bba)*bbb)L(0) + a(a + ba + bba)*bb

L(0)= (b + a(a + ba + bba)*bbb)*a(a + ba + bba)*bb

Cette expression régulière semble difficile à simplifier, toutefois essayons de démontrer qu’elle est bien égale à (a + b)*abb.

Supposons donc :

(a + b)*abb = (b + a(a + ba + bba)*bbb)*a(a + ba + bba)*bb

si on supprime « bb » de part et d’autre, on a l’égalité :

Þ (a + b)*a = (b + a(a + ba + bba)*bbb)*a(a + ba + bba)*

Þ (a + b)*a = (b + a((e + b + bb)a)*bbb)*a((e + b + bb)a)*

Þ (a + b)*a = (b + (a(e + b + bb))*abbb)*(a(e + b + bb))*a

car x(yx)* = (xy)*x

si on supprime « a » de part et d’autre, on a l’égalité :

Þ (a + b)* = (b + (a(e + b + bb))*abbb)*(a(e + b + bb))*

Þ (a + b)* = (b + (a + ab + abb)*abbb)*(a + ab + abb)*

Þ (a + b)* = b*((a + ab + abb)*abbbb*)*(a + ab + abb)*

car (x + y)* = x*(yx*)*

Þ (a + b)* = b*((a + ab + abb) + abbbb*)*

car (x*y)*x* = (x + y)*

Þ (a + b)* = b*(a + ab + abb + abbbb*)*

Þ (a + b)* = b*(a (e + b + bb + bbbb*))*

Þ (a + b)* = b*(a b*)*

ce qui est vrai car (x + y)* = x*(yx*)*

Donc on a bien :

(a + b)*abb = (b + a(a + ba + bba)*bbb)*a(a + ba + bba)*bb

Donc l’automate reconnaît bien le langage (a + b)*abb

<

4 Dans l’exemple précédent, nous avons supposé que :

X* = (e + X + XX + XXXX*)

Pouvez-vous le démontrer ?

Pouvez-vous démonter le cas général : X* = (e + X + XX + XXX + … + XⁿX*)

Réponses :

X* = (e + X + XX + XXX(e + X + XX + …))

(e + X + XX + XXX + XXXX + XXXXX + …)

X*

X* = (e + X + XX + XXX + … + XⁿX*)

(e + X + XX + XXX + … + Xⁿ(e + X + XX + …))

(e + X + XX + XXX + … + Xⁿ + XⁿX + XⁿXX + …)

(e + X + XX + XXX + … + Xⁿ + Xⁿ⁺¹ + Xⁿ⁺² + …)

X*

On remarquera que X* = (X*)ⁿ = (X*)*

3

4 Dans l’exemple précédent, plusieurs fois, on a supprimé un mot de part et d’autre d’une égalité afin de la démontrer. Dans quel cas ne peut-on pas le faire et pourquoi ?

Vérifier que (a + b)*ab(a +b)* = b*a*ab(a+b)*

Avons-nous (a + b)*ab = b*a*ab ? Expliquez.

3

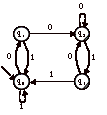4 Soit l’automate A suivant :

Produisez l’expression régulière de A à l’aide de la méthode de résolution d’équations. Quel langage reconnaît cet automate ?

Réponse (non détaillée) : il s’agit de tous les mots sur {0, 1} sauf 11.

3

4. Déterminisation & Minimisation

4.1. Méthode de déterminisation

Si dans un automate A, il existe deux chemins q₀…q_n et q₀…q_m décrivant le même mot alors ces deux chemins appartiennent à la même classe d’équivalence. Ils peuvent donc être regroupés en un seul chemin pour ce mot. Cette constatation est à la base de la méthode déterminisation.

Propriété :

Pour tout automate d’états finis non-déterministe, il existe un automate d’état fini déterministe équivalent.

Soit A = (V_T, Q, Q₀, F, m) un AEF non-déterministe

Alors A’ = (V_T, P(Q), Q₀, F’, m’)

avec F’ = {Q’’ | Q’’ Ç F ≠ Æ}

Alors L(A) = L(A’)

4 Démonstration de la propriété ci-dessus

3

La méthode consiste à définir des transitions sur des ensembles d’états et non des états. À partir d’un ensemble d’états, on définit l’ensemble successeur pour un x de V comme l’ensemble des états atteignables par x depuis un état de l’ensemble. Seule une partie des sous-ensembles possibles est utile. Pour calculer les sous-ensembles utiles, on itère jusqu’à ce que aucun nouveau sous-ensemble soit créé. L’ensemble de départ est l’ensemble des états initiaux. Chaque ensemble d’états correspond à un état de l’automate déterministe. Un état est final si un des états d’origine le composant est final.

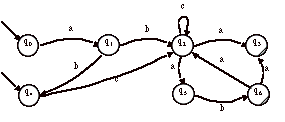> Soit par exemple, A l’automate non-déterministe suivant :

Nous obtenons la table de transitions suivantes :

		a	b	c
® 0	{0, 4}	{1}	-	{2}
1	{1}	-	{2, 4}	-
2	{2}	{3, 5}		{2}
3	{2, 4}	{3, 5}	-	{2}
¬ 4	{3, 5}	-	{6}	-
¬ 5	{6}	{2, 3}	-
¬ 6	{2, 3}	{3, 5}	-	{2}

<

4 Créer la table de transitions de l’automate non-déterministe. Dessiner et commentez l’automate déterministe ci-dessus.

3

4.3. Relation d’équivalence sur les langages réguliers

À partir de la notion d’automate, on peut définir une relation d’équivalence sur les mots de V_T*.

Si deux mots distincts conduisent dans un automate A à l’état q_i, alors ces deux mots sont équivalents.

Définition : w₁ » w₂ Û " z Î V_T*, w₁z Î L Û w₂z Î L

La relation » est réflexive w₁ » w₁

La relation » est symétrique w₁ » w₂ Þ w₂ » w₁

La relation » est transitive w₁ » w₂, w₂ » w₃ Þ w₁ » w₃

Soit un automate A reconnaissant le langage L.

Relation réflexive :

w Î L(A) Û (q₀, w) a* (q, e) q Î F

Par définition de a* (q₀, w₁) a* (q, e) Þ (q₀, w₂) a* (q, e)

donc w₁ » w₁

Relation symétrique :

w₁ » w₂ :

" z Î V_T* (q₀, w₁z) a* (q,, e) q Î F

Û (q₀, w₂z) a* (q’, e) q’ Î F

donc " z Î V_T* (q₀, w₂z) a* (q’, e) q’ Î F

Û (q₀, w₁z) a* (q,, e) q Î F

donc w₂ » w₁

Relation transitive :

w₁ » w₂ et w₂ » w₃ :

w₁ » w₂ : " z Î V_T* (q₀, w₁z) a* (q,, e) q Î F

Û (q₀, w₂z) a* (q’, e) q’ Î F

w₂ » w₃ : " z Î V_T* (q₀, w₂z) a* (q,, e) q Î F

Û (q₀, w₃z) a* (q’, e) q’ Î F

" z Î V_T* (q₀, w₁z) a* (q, e) q Î F

Û (q₀, w₂z) a* (q’ e) q’ Î F

Û (q₀, w₃z) a* (q’’ e) q’’ Î F

> Soit, par exemple, l’automate suivant :

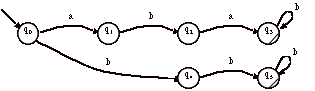
Les états q_{2 et} q₄ sont »

Soient les mots ab et b, ils sont »

En effet, pour q₂ : (q₀, ab) a (q₂, e)

Ensuite un mot appartient à L si et seulement si, il est de la forme ab*

pour q₄ : (q₀, b) a (q₄, e)

Ensuite un mot appartient à L si et seulement si, il est de la forme ab*

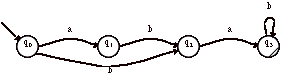Nous aurions pu définir l’automate :

La relation d’équivalence nous permet de définir un automate ayant un nombre minimum d’états.

ici on n’a pas e » a car e.aba Î L

a.aba Ï L

Donc q₀ et q₁ n’appartiennent pas à la même classe d’équivalence. <

Une relation d’équivalence est invariante à droite si et seulement si :

" w₁,w₂ Î V_T* w₁ » w₂ Þ " z Î V_T* w₁z » w₂z

Les propriétés suivantes sont équivalentes :

a) le langage L est reconnu par un automate d’états fini ;

b) le langage L est la réunion d’un ensemble de classes d’équivalence d’une relation d’équivalence invariante à droite d’index fini.

Démonstration :

1) a Þ b

Soit A un automate d’états fini tel que L = L(A).

Alors soit R la relation :

w₁ Â w₂ Û (q₀, w₁) a* (q, e) Ù

(q₀, w₂) a* (q, e)

 est un relation d’équivalence réflexive, symétrique et transitive.

Soit [q] la classe d’équivalence définie par :

w Î [q] Û (q₀, w) a* (q, e)

Alors

 est d’indice fini.

2) b Þ a

Soit  la relation d’équivalence. On défini donc un automate d’état fini tel que :

Q = {[w] | w Î V_T*} l’ensemble des classes

Q est fini car l’indice de la relation est fini.

A = (V_T, Q, [e], F, m)

F = {[w] | w Î L]

m : m([w], s) = [ws]

donc " z Î V_T* ([e], w) a* ([w], e)

et w Î L Û [w] Ì L

4 soit L le langage sur {a, b} dont les mots contiennent au moins un « ab ». Donnez une expression régulière simple de ce langage. Construisez les automates non-déterministe et déterministe.

Quels états de l’automate déterministe peut-on regrouper dans de mêmes classes d’équivalence ?

Réponses : (peu détaillée)

R(L) = (a + b)*ab(a + b)*

On a comme automates A et Adet :

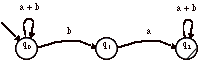
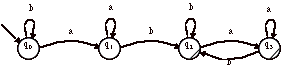
Pour avoir si deux état de Adet sont équivalents, posons et résolvons les équations d’états pour Adet :

L₀ = bL₀ + aL₁

L₁ = aL₁ + bL₂

L₂ = bL₂ + aL₃ + e

L₃ = bL₂ + aL₃ + e

On constate que L₂ = L₃. Ici, on n’a pas besoin de résoudre l’équation pour constater que les deux langages sont égaux, car les parties droites des équations sont identiques. Toutefois on gardera à l’esprit, que si deux équations sont différentes, il est possible que leurs solutions soient égales.

Si on résout L₃

L₃ = a*(bL₂ + e)

Donc

L₂ = bL₂ + aa*(bL₂ + e) + e

L₂ = (b + aa*b)L₂ + aa* + e

L₂ = (b + aa*b)*(aa* + e)

Donc

L₂ = (b + aa*b)*a* = (( e + aa*)b)*a* = (a*b)*a* = (a + b)*

On obtient bien la même chose pour L₃.

On peut donc simplifier l’automate Adet en Adet’ :

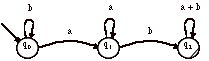
Vérifiez si l’automate peut être simplifié plus avant.

3

4 soit L’ le langage décrit par l’expression régulière b*a*ab(a+b)*.

Montrer que L’ est équivalent au langage L de l’exercice précédent.

Commentez.

3

5. Autres opérations sur les automates

5.1. Automate complémentaire ¬A

Il peut être difficile de trouver à partir de l’expression régulière le complémentaire ¬L d’un langage régulier L. Par contre, produire le complémentaire ¬A d’un automate régulier déterministe A est aisé.

Pour produire à partir de A (qui reconnaît le langage L(A)) l’automate complémentaire ¬A reconnaissant le langage complémentaire ¬(L(A)), il suffit de :

Créer un état trappe T ;

Soit v_i les éléments du vocabulaire V sur lequel est défini L(A). Pour chaque état q, créer une transition v_i de q vers T s’il n’existe pas de transition v_i partant de q ;

Chaque état final devient ordinaire et chaque état ordinaire devient final. L’état initial reste initial. L’état trappe T devient final.

Si l’état trappe T n’est pas relié, il pourra être supprimé.

> Soit, par exemple, L le langage sur V = {a, b, c} composé de mots composé que de a ou de b et contenant une fois une séquence de 0 ou n « c ». Essayons de produire l’expression régulière de ¬L.

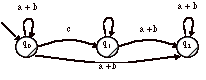L’expression régulière R(L) est (a + b)*c*(a + b)* et l’automate non-déterministe est :

c

L’automate déterministe équivalent est :

		a	b	c
® ¬ 0	{0}	{0, 2}	{0, 2}	{1}
¬ 1	{0, 2}	{0, 2}	{0, 2}	{1}
¬ 2	{1}	{2}	{2}	{1}
¬ 3	{2}	{2}	{2}	-

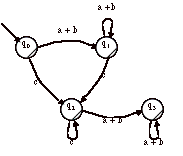
On créé un état trappe T et on sature les transitions de l’automate vers cet état. Le langage est inchangé.

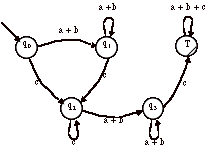On inverse les états finals et non-finals. L’automate obtenu reconnaît ¬L.

L’expression régulière peut être trouvée par la méthode des équations d’états. L’automate est saturé, chaque équation comportera trois termes (pour a, b et c) pour un état ordinaire et on rajoutera e pour les états finals.

a) L₀ = (a + b)L₁ + cL₂

b) L₁ = (a + b)L₁ + cL₂

c) L₂ = (a + b)L₃ + cL₂

d) L₃ = (a + b)L₃ + cL_T

e) L_T = (a + b + c)L_T + e

L_T = (a + b + c)* = V*

L₃ = (a + b)*cL_T

= (a + b)*c(a + b + c)*

L₂ = c*(a + b)L₃

= c*(a + b)(a + b)*c(a + b + c)*

L₁ = (a + b)*c L₂

= (a + b)*cc*(a + b)(a + b)*c(a + b + c)*

L₀ = L₁

= (a + b)*cc*(a + b)(a + b)*c(a + b + c)*

Il s’agit du langage des mots quelconques sur {a, b} qui comportent au moins 2 séquences non nulles de c.

Il s’agit bien du complémentaire du langage qui comporte une seule séquence éventuellement nulle de c.

D’après les équations ci-dessus, on s’aperçoit que q₀ et q₁ sont dans la même classe d’équivalence. On peut donc simplifier l’automate :

<

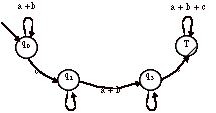
4 Décrire et caractériser la classe des automates réguliers invariants par l’opération de complémentation. Commentez.

3

4 L’opération de complémentation fonctionne-t-elle sur des automates non-déterministe ? Commentez.

3

5.2. Automate miroir A~

Pour produire à partir de A (qui reconnaît le langage L(A)) l’automate miroir A~ reconnaissant le langage miroir (L(A))~, il suffit de :

Inverser le sens des transitions ;

Échanger les états initiaux et les états finals ;

Déterminiser l’automate produit (si nécessaire).

On notera que L(A~) = L(A)~. Il s’agit juste d’un jeu d’écritures.

L’opération consistant à inverser le sens des transitions, peut à partir d’un automate déterministe produire un automate non-déterministe.

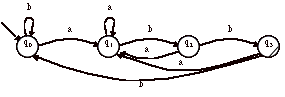> Par exemple, soit l’automate A suivant :

Cet automate est l’automate déterministe reconnaissant les mots de la forme :(a + b)*abb

Après inversion des transitions et des états, nous avons l’automate miroir non-déterministe (A~)_ndet suivant :

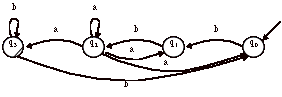
L’automate déterministe A~ équivalent est :

		a	b
® 0	{0}	-	{1}
1	{1}	-	{2}
3	{2}	{0, 1, 2, 3}	-
¬ 3	{0, 1, 2, 3}	{0, 1, 2, 3}	{0, 1, 2, 3}

Cet automate est déterministe et reconnaît les mots de la forme bba(a + b)* = ((a + b)*abb)~

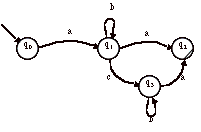On remarquera que si on cherche à produire l’image miroir de l’automate ci-dessus, c’est-à-dire (A~)~, on obtiendra avant déterminisation l’automate non-déterministe du langage (a + b)*abb. <

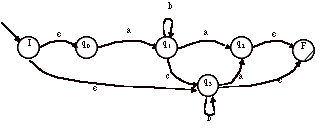
4 soit l’automate A ci-contre :

Trouver l’expression régulière du langage reconnu par A.

Construire l’automate A~ et trouver l’expression du langage reconnu.

Commentez.

Réponses  L’expression régulière correspondante est R(A) = ab*a + ab*cb*a = ab*(a + cb*a). Si on inverse le sens des flèches et que les états initiaux deviennent finals et que les états finals deviennent initiaux alors on obtient :

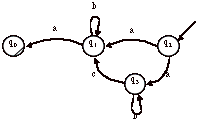
L’automate non-déterministe miroir A~ est (après avoir renommé les états) :

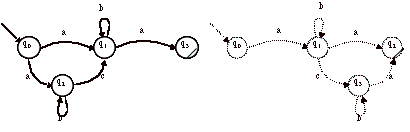
L’expression régulière R(A~) est : ab*a + ab*cb*a

On remarque ici que R(A~) = R(A), donc L(A~) = L(A), donc L(A) = L(A)~. Le langage L(A) est donc un langage dont l’expression régulière est une union de palindromes. Ceci ne veut pas dire que les mots de L(A) sont nécessairement des palindromes.

La version déterministe de cet automate est :

		a	b	c
® 0	{0}	{1, 2}	-	-
1	{1, 2}	{3}	{1, 2}	{1}
2	{1}	{3}	{1}	-
¬ 3	{3}	-	-	-

Il s’agit du même automate que A.

3

4 Est-il possible d’obtenir un automate déterministe à partir d’un automate non-déterministe après inversion des transitions ? Et à partir d’un automate déterministe ?

3

4 Décrire et caractériser la classe des automates réguliers invariants par l’opération miroir.

3

5.3. Intersection de deux automates

La production de l’expression régulière du langage L = L₁ Ç L₂ à partir des expressions régulière de L₁ et L₂ n’est pas aisée. Par contre, il existe une méthode simple pour construire l’intersection de deux automates déterministes A₁ et A₂.

Un mot appartient à deux automates déterministes A₁ et A₂ si on est capable de suivre dans les deux automates un chemin décrivant ce mot de l’état initial à un état final.

A₁= (V_T1, Q₁, Q₀₁, F₁, m₁) et A₂= (V_T2, Q₂, Q₀₂, F₂, m₂)

w Î L(A) = L(A₁ Ç A₂) si et seulement si :

$ (q,q’) Î F₁ ´ F₂ : ((q₀₁,q₀₂), w) a* ((q,q’), e)

Le mot w appartient au langage reconnu par l’automate A s’il existe un chemin de l’état initial à un état final qui décrit ce mot à la fois dans A₁ et A₂.

La construction de A = A₁ Ç A₂ consiste à parcourir en parallèle les deux automates, et à ne retenir comme état que les couples d’états atteignables à la fois dans les deux automates.

Un état q du nouvel automate A sera final si les deux états (q’, q’’) issus de A₁ et A₂ sont finals.

> Exemple : Soit L_a2, le langage sur {a,b} composé de n « a », ou n est un multiple de 2. Soit L_a3, le langage composé d’une succession de n « a », ou n est un multiple de 3.

Quelle est l’intersection de L_a2 et L_a3 ?

R(L_a2) = b*(ab*ab*)* et R(L_a3) = b*(ab*ab*ab*)*

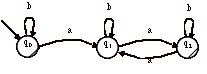
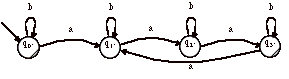
On obtient la table de transitions suivante :

		a	b
® 0	(0,0’)	(1, 1’)	(0, 0’)
1	(1, 1’)	(2, 2’)	(1, 1’)
2	(2, 2’)	(1, 3’)	(2, 2’)
3	(1, 3’)	(2, 1’)	(1, 3’)
4	(2, 1’)	(1, 2’)	(2, 1’)
5	(1, 2’)	(2, 3’)	(1, 2’)
¬ 6	(2, 3’)	(1, 1’)	(2, 3’)

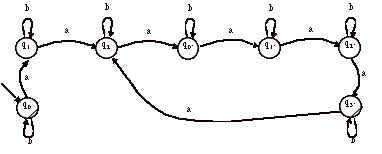
R(A) = b*(ab*ab*ab*ab*ab*ab*)*

Il s’agit du langage L_a6.

<

4 D’une façon générale, que peut-on dire de L_an Ç L_am (n³1 et m³1) ?

Calculez également L_a2 Ç L_b2 et généralisez vos résultats.

Réponses : A(L_a2 Ç L_b2) à 9 états et reconnaît les mots ou le nombre de a et le nombre de b sont pairs.

Un automate L_an a n+1 états. A(L_an Ç L_bm) à (m + 1)*(n + 1) états.

La définition fonctionnelle de A(L_a2 Ç L_b2) est :

V= {a, b} F = {6, 7, 8} Q₀ = {0} Q = {0, 1, 2, 3, 4 5, 6, 7 ,8}

d(0,a) = 1 d(0,b) = 2 d(1,a) = 3 d(1,b) = 5

d(2,a) = 5 d(2,b) = 4 d(3,a) = 1 d(3,b) = 7

d(4,a) = 6 d(4,b) = 2 d(5,a) = 7 d(5,b) = 6

d(6,a) = 8 d(6,b) = 5 d(7,a) = 5 d(7,b) = 8

d(8,a) = 6 d(8,b) = 7

3

4 On appelle A(f), la classe d’automates n’acceptant aucun mot. Quelle est la propriété suffisante pour qu’un automate appartienne à A(f). Quelle propriété doivent vérifier les automates pour qu’elle soit aussi nécessaire ?

Montrer que cette classe d’automates réguliers est infinie.

Montrer que quelque soit A, on a : A Ç ¬A Î A(f).

3

6. Conclusion

Nous avons introduit dans ce chapitre le concept d’automate à état finis régulier. Ce type de machine abstraite est équivalent aux langages réguliers et aux expressions régulières. Cependant, un certain nombre d’opérations de manipulation se font aisément sur les automates, ce qui n’est pas nécessairement le cas sur les expressions régulières.

Exercices

1. Construisez l’automate déterministe qui accepte les mots sur V={a, b} tels que le nombre de a soit pair.
Même question avec un nombre de a impair.

2. Construisez l’automate déterministe qui accepte les mots sur V={a, b} tels que le nombre de a soit pair et le nombre de b pair.
Même question avec : a pair et b impair ; a impair et b pair ; et a et b impair.

3. Construisez les automates non-déterministe et déterministe qui accepte L dont les mots sur V={a, b, c, d} ne se terminant que par abc.
Retrouvez à partir de l’automate l’expression régulière de ce langage.

Même questions avec ¬L, L~, (¬L)~, ¬(L~) et ¬L Ç (¬L)~

4. Construisez systématiquement l’automate à partir des expressions régulières suivantes : a. ((ab)*b*)* b. (abb*)* c. ((a*b)*b)*
Essayez de réduire la taille des automates obtenus. Produisez des versions non-déterministes.

5. Construisez les automates des deux expressions régulières suivantes :
L1 = a*ba* et L2 = b*ab*
Construisez l’automate de L = L1 Ç L2. Retrouver R(L).

6. Décrivez un algorithme qui permet de tester si le langage reconnu par un automate régulier donné est vide, fini non vide, ou infini.

7. (Lemme de l’étoile) Démontrez que pour tout langage régulier L, il existe un entier N tel que tout mot w de L de longueur |w| ³ N admet une factorisation w = uxv avec 0 <|x|< N et vérifiant ux*v Ì L.

8. Utilisez le lemme de l’étoile pour prouver que les langages suivants ne sont pas réguliers : {aⁿbⁿ | n ³ 0} {aⁿb^p | n ³ p ³ 0} {aⁿb^p | n ¹ p}

9. Montrez prouver que les langages suivants ne sont pas réguliers :
{a^2¨n | n ³ 1} {a^p | p premier} {a^n! | | n ³ 1}

10. Montrez que les deux automates suivants reconnaissent le même langage : Construire l’automate déterministe reconnaissant le même langage. Retrouver l’expression régulière de ce langage à partir de l’automate déterministe.









Plus généralement, montrer que les langages V*wVⁿ, avec V={a, b}, n> 0 sont reconnu par au moins |w| + 1 automates non déterministe non isomorphes ayant strictement moins d’états que l’automate déterministe minimal de ce langage.

11. Soient deux automates A et A’. On se propose de tester si ces deux automates sont équivalents, c’est-à-dire qu’ils reconnaissent le même langage. Donnez une méthode basée sur l’opération d’union d’automates.

12. Décrivez pour l’automate ci-dessous le langage L qu’il reconnaît. Produisez son expression régulière. Produisez un automate non-déterministe, plus petit (si possible).
Peut-on produire un automate déterministe plus petit ?

13. Soit l’opération de différence (notée \) définie sur les langages de la même façon qu’elle est définie sur les ensembles (A \ B = A Ç ¬B). L \ L’ est l’ensemble des mots de L moins les mots de L’.
Expliquez pourquoi si L et L’ sont des langages réguliers, L \ L’ est bien un langage régulier.

En passant par les automates, expliquez comment on peut trouver L \ L’.

Appliquer votre méthode aux exemples suivants :
(ab)*a \ a*(ba)* b*(ab*ab*)* \ a*b(ba*ba*)*
Commentez.

14. La séquence « 527943001 » est la liste des chiffres qui apparaissent dans les colonnes quand on pose l’addition :

95
+ 42
137

Nous avons rempli les colonnes avec des 0 si nécessaire. Construisez un automate qui accepte les séquences qui correspondent à des additions correctes et rejètent les autres.

Une version plus simple, consiste à construire l’automate pour les additions de nombres binaires uniquement.

15. Montrez que le langage sur V={a, b} ne contenant pas trois a de suite est régulier. Construire les automates non-déterministes, déterministes et (au moins) une expression régulière.

16. Montrez que si un automate déterministe A accepte un mot dont la longueur est supérieure au nombre d’états de A, alors A accepte un nombre infini de mots.

17. Trouvez une expression régulière qui représente les langages suivants :
(a + b*) Ç (a + b)* a(a + b)* Ç (a + b)*b
(a + b)b(a + b)* Ç b(a + b)* (ab)*(a + f) Ç (a + b)(ab)*

18. Montrez que si L est un langage régulier qui ne contient pas e, alors L peut être reconnu par un automate régulier non-déterministe avec un seul état d’acceptation.

19. Construisez un automate A sur V = {a, b, c, d} qui reconnaît un langage dont les mots ont les propriétés suivantes : le sous-mot « ab » est toujours suivi de « c », et le sous-mot « ba » est toujours suivi de « d ».

20. Construisez un automate A sur V = {a, b} qui reconnaît un langage dont les mots ne contiennent jamais la sous-chaîne « bab ».

21. Soit X, Y Í V*. On définit XY-1 = {w | wy Î X pour y Î Y)
Montrer que si X est régulier alors XY^-1 est régulier.

n n n

n n

n