Document utile au démarrage

• Animation - tutorial sur les timing functions
• Courbes - résumé de notions utiles

Animation d'attributs graphiques

Le but de cet exercice est de mettre en oeuvre trois stratégies différentes d'interpolation d'une valeur représentée par un nombre flottant variant entre a0 (valeur initiale) et a1 (valeur finale).

Envisager les trois méthodes vues en cours:

• Interpolation avec ralenti à l'arrivée
• Interpolation linéaire (à vitesse constante)
• Interpolation avec vitesse variable (lent, vite, lent) et accélération constante au signe près.

Pour chaque type d'interpolation, afficher la courbe des valeurs interpolées entre 0 et 2 * π ou entre 0 et 1.

Courbes paramétrées définies par morceaux

On considère les fonctions paramétrées suivantes

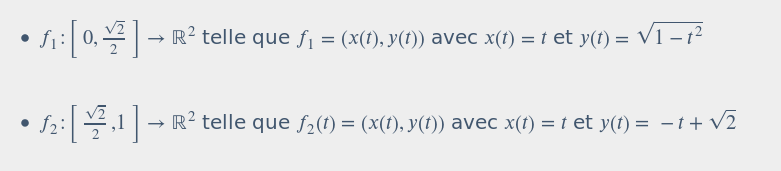
• Quelle est la nature de la courbe représentée par f₁?
• Quelle est la nature de la courbe représentée par f₂?
• La courbe construite à partir de la concaténation de f₁ et f₂ est-elle de classe C1? est-elle de classe C2?
• Construire et afficher cette courbe.

Courbes paramétrées polaires

Cet exercice a pour objectif la construction et l'affichage des deux courbes paramétrées polaires définies par:

• ρ₁(t) = a * t avec t ∈ [0, 2 π]
• ρ₂(t) = a * e^bt avec t ∈ [0, 2 π]
• ρ₃(t) = sin(2*t) et θ₃(t) = cos(3*t) avec t ∈ [0, 2 π]
• ρ₄(t) = a * cos(2*t) avec t ∈ [0, 2 π]
• ρ₅(t) = a * cos(7*t) avec t ∈ [0, 2 π]

Dans cet exercice, a et b sont des paramètres qui permettent de définir des familles de courbes.

Repère mobile, et déplacement des objets le long de courbes

Les objets utilisés au tp précédent peuvent être réutilisés dans ce tp. L'objectif de cet exercice est de représenter ces objets dans un repère mobile pour qu'ils puissent se déplacer le long des courbes suivantes. Pour chaque courbe, afficher la courbe et animer l'objet qui se déplace le long de cette courbe.

1. La courbe de la fonction sinus
2. La courbe de la fonction racine
3. La courbe de la fonction carré
4. les courbes définies aux exercices précédents

Question subsidiaire: composer un mouvement local de l'objet dans son repère (une rotation sur son centre) avec un mouvement le long de la trajectoire.

Mini-éditeur d'animations 2D

Le but de cet exercice est de construire une application interactive qui permette à un utilisateur de réaliser des animations simples.

Dans la première partie, il s'agit d'animer la position d'objets graphiques simples et prédéfinis dans leur repère en suivant une courbe choisie parmi les courbes étudiées dans les exercices précédents de ce td. En option, on pourra ajouter l'animation de la position des objets selon de nouvelles courbes, définies en extension ou en compréhension par l'utilisateur.

Dans la deuxième partie, on souhaite animer la transformation d'objets graphiques simples et prédéfinis dans leur repère en fonction d'une séquence de transformations affines.

Dans la troisième partie, il s'agit d'animer des attributs graphiques de l'objet tels que taille, couleur, et visibilité en complément des attributs de position x et y. Dans cette troisième partie, on utilisera les résultats de l'exercice 3 pour interpoler les valeurs des attributs entre les valeurs données pour le début de l'animation et les valeurs données pour la fin de l'animation.

Enfin, une partie optionnelle de ce mini-éditeur est envisageable lorsque les trois premières parties sont réalisées. Cette partie optionnelle consiste à étudier l'un des principes usuels de conception d'animations, tels, par exemple, que ceux décrits dans l'article de John Lasseter, "Principles of Traditional Animation Applied to 3D Computer Animation", Computer Graphics, pp. 35-44, 21:4, July 1987 (SIGGRAPH 87). Dans cette partie optionnelle, il s'agit, par exemple d'étudier et de mettre en oeuvre un principe d'animation sur un exemple simple comme par exemple le rebond d'un objet souple ou articulé avec le principe de "squash and stretch" ou l'animation d'un objet avec dépendances pour le principe du "follow through".