Quartets
are bifurcating trees
on four-taxa subsets that can be combined into on overall tree on the
set of all studied taxa. For four specific taxa x,y,z,t, there
are 3 different quartets:
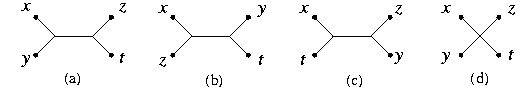corresponding to the 3 possible phylogenetic assumptions.
Quartet-based methods operate in two phases to infer a tree
from a molecular or distance dataset:
- Inference of a set of quartets: for each set of four taxa,
a quartet is chosen (sometimes several are included, indicating indecision).
- Inference of tree from the previously inferred set of
quartets: the prefered tree is the one agreeing (ie satisfying) with
the greatest number of input quartets. However, finding this tree is
an NP-difficile problem (ie requires an time exponential in the number
of taxa) and either heuristics are used (such as Quartet Puzzling of
[Strimmer,von Haeseler 96]) either other reconstruction criteria
(e.g., the Disc-cover method of [Warnow et al 98]). Among
the latter, the Q* method is one of the few method which is
using a criteria that can be computed exactly in polynomial time.
Last modified: Thu Mar 11 10:51:25 MET DST 1999