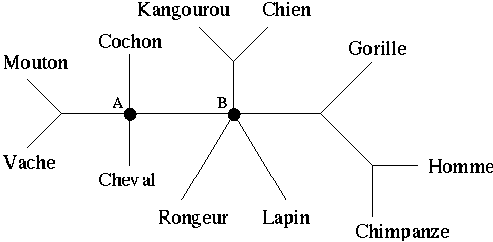
Figure 1 : Exemple de squelette de phylogénie (l'arbre n'est pas
binaire : les noeuds A et B sont de degré > 3).
Encadrant : Vincent Berry
Équipe
Méthodes et algorithmes pour la bioinformatique, IFA
Ce stage se situe dans le domaine de l'algorithmique appliquée à la biologie, et aborde le problème de la construction d'arbres modélisant l'évolution des espèces (cf module de Bioinformatique du DEA).
Un arbre d'évolution, aussi appelé phylogénie est un arbre (graphe connexe sans cycle) dont les feuilles sont chacune étiquetée par une espèce (animale ou végétale) actuelle. Les sommets internes correspondent à des espèces ancestrales, et ne sont pas étiquetés. La structure de l'arbre (l'agencement des arêtes et des feuilles) indique les groupes d'espèces apparentées.
Le problème abordé dans ce stage est l'affinage de phylogénies
non binaires :
les biologistes supposent que les espèces ont émergé les unes après les autres des espèces ancestrales, et non qu'une espèce ancestrale a pu donner naissance au même moment à 3,4 nouvelles espèces. Concrêtement, ça signifie qu'on cherche toujours à inférer des phylogénies commplètement binaire (le degré des sommets internes est égal à 3).
La méthode Q* que nous avons proposée récemment permet d'inférer un squelette de la phylogénie correcte, ie une phylogénie dont chaque arête a très peu de chances d'être incorrecte (cf nos simulations et celles d'autres auteurs).
Toutefois, comme son nom l'indique, ce squelette de phylogénie n'est pas complètement résolu, ce qui signifie qu'il possède des sommets de degré supérieur à trois. Ces sommets doivent être résolus, ce qui signifie que les différents sous-arbres connectés à ces noeuds doivent être regroupés pour obtenir une phylogénie binaire. Autrement dit, l'arbre doit être affiné.
La figure 1 montre un squelette d'arbre obtenu depuis un jeu de données sur les mammifères :

Figure 1 : Exemple de squelette de phylogénie (l'arbre n'est pas
binaire : les noeuds A et B sont de degré > 3).
Le problème considéré dans le stage est de définir une méthode pour affiner un squelette d'arbre, en suivant un principe traditionnel de construction de phylogénies pour choisir entre les différents affinages possibles.
Des résultats positifs de ce côté déboucheraient à coup sûr sur une publication.
Le stage se déroulera au sein de l'équipe Méthodes et
algorithmes pour la bioinformatique, composée de Gilles
Caraux (ENSAM), Olivier Gascuel (CNRS), Eric Rivals (CNRS), Vincent
Berry (UM II) et de 5 thésards en bioinformatique.
Des documents sur la reconstruction de phylogénies ainsi que des informations sur l'équipe peuvent être trouvés depuis la page de l'équipe MAB ou la mienne
Translated with latex2html