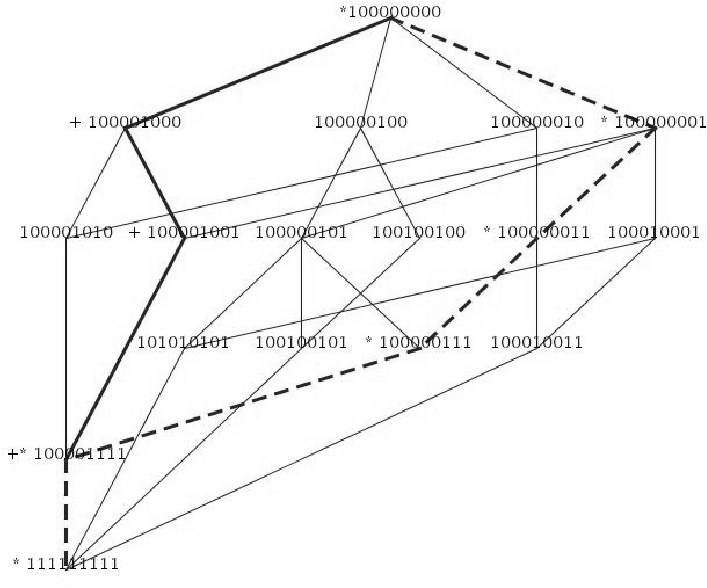
Figure 1: A representation of the lattice
Γ(9). The bold-edges and dashed-edges paths shows two maximal
chains of different lengths between 111111111 and 100000000. The
correlations on these paths are marked with a + or a *,
respectively.
Autocorrelation of Strings
|
| Offset: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |||||||||
| A | B | R | A | C | A | D | A | B | R | A | ⋮ | ⋮ | ||||||||
| A | B | R | A | C | A | D | A | B | R | A | ⋮ | |||||||||
| A | B | R | A | C | A | D | A | B | R | A | ||||||||||
| Autocorrelation: | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||||
| Offset: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Word | a | b | a | b | a | b | a | b | a |
| Period 2 | a | b | a | b | a | b | a | ||
| Period 4 | a | b | a | b | a | ||||
| Period 6 | a | b | a | ||||||
| Period 8 | a | ||||||||
| Autocorrelation | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Moreover, we have also noticed that the complete set of periods is redundant and have defined the Irreducible Periods Set, which is the smallest subset of the periods set whose enable to recompute the periods set. There is a one-to-one (bijective) correspondance between periods sets and Irreducible Periods Sets.
Figure 1: A representation of the lattice Γ(9). The bold-edges and dashed-edges paths shows two maximal chains of different lengths between 111111111 and 100000000. The correlations on these paths are marked with a + or a *, respectively.
|
+o(1) ≤ |
|
≤ |
|
+o(1). (1) |
We have that the number of autocorrelations of length n, κn, is bounded by the number of autocorrelations of length n whose basic period is larger than n/2. The latter equals the sum of the κi for i going from 0 to ⌈ n/2 ⌉ −1. Thus, we define L0:=1, L1:=1, and, for n≥ 2, Ln := Σi=0⌈ n/2 ⌉ −1 Li. By induction, Ln≤ κn for all n≥ 0.
Figure 2: True values of lnκn/(lnn)2 for n≤ 400, compared to Guibas & Odlyzko's (G&O) asymptotic lower bound, the improved asymptotic bound from Theorem 1 (ii) derived from DeBruijn's results, and the non-asymptotic lower bound from Theorem 1 (i) based on Fröberg's work. Both of these bounds converge to the G&O asymptotic value of 1/(2 ln2) for n→∞. The upper bound of G&O, corresponding to the line y=1/(2 ln(3/2))≈ 1.23, is not visible on the figure.
|
≥ |
|
⎛ ⎜ ⎜ ⎝ |
1− |
|
⎞ ⎟ ⎟ ⎠ |
|
+ |
|
− |
|
+ O | ⎛ ⎜ ⎜ ⎝ |
|
⎞ ⎟ ⎟ ⎠ |
. |
| Nk=σρk − |
|
Nj. |
This document was translated from LATEX by HEVEA.