Unifying Theories for Multivariate Algorithms (ANR-DFG project, ANR-20-CE92-0027) Studying the tractability of computational problems is a core challenge in theoretical computer science. A central question

Efficiency and Structure in Graph Mining Application (ANR-17-CE23-0010). As a general modelling tool, graphs are gaining increasing attention. They capture the interactions of entities in an easily comprehensible way and yet provide a rich model of the underlying structure. As information technology scrapes up ever more data in diverse areas of human activities, it becomes vital to discover meaningful information from the massive amounts of available data. Data sets can

Decomposition of graphical models (ANR-16-CE40-0028) Solving NP-hard problems is still a challenge at the theoretical or practical level. This project aims at solving decision, optimization and counting (discrete integration) problems defined as “graphical models” (constraint or cost function networks, bayesian networks, propositional logic and Markov random fields). In such models, a joint function over a set of variables is described as a factorized combination of functions of few variables. This

KERNEL (Languedoc-Roussillon Regional grant “chercheur d’avenir) Massive datas arise from most of the scientific disciplines, including biology, physics, environmental and health science… To handle the huge amount of (hidden) information represented by these datas require a systematic and rigorous approach ranging from databases and data mining to algorithms. A key to improve the algorithmic efficiency is to simplify, to filter, to reduce the given data sets. Underlying most of the

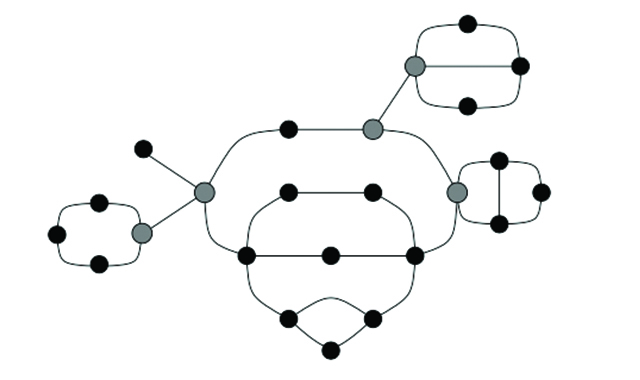
Efficient algorithms for graph modification problems (AURORA French-Norwegian project) Despite the simplicity of their definition, graphs are fundamental objects for computer science. On one side, they are the basis of a number of models in many different application areas (networks, biology, molecular chemistry). On the other side, they capture a large part of the computational complexity. A way to understand the graph structure is to study the combinatorial structure of

Exact and parameterized algorithms (ANR-09-BLAN-0159) In the classical complexity theory, a problem is considered to be non-tractable if it cannot be solved in polynomial time. But lots of real world problems are naturally modelled by graph optimisation problems which are NP-hard that is for which no polynomial time algorithm exists (unless P=NP). Hence, finding solutions to these problems is an important issue. Sometimes approximate (but non-optimal) solutions are sufficient but

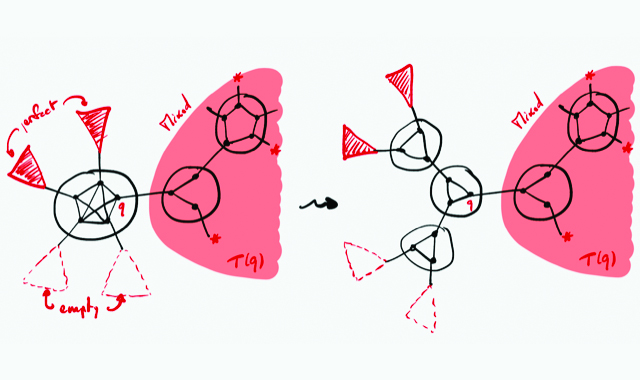
Graph decomposition and algorithms (ANR-06-BLAN-0148) This project deals with fundamental aspects of computer science, namely theoretical and algorithmic aspects of decomposition methods for graphs and various combinatorial structures and extensions such as matroids, countable graphs… We propose to combine approaches issued from graphs, discrete algorithms, formal languages and logic theory. We believe that major contributions to decomposition methods are no longer possible if each of these theories is considered separately.