Bijections on 4-realizers

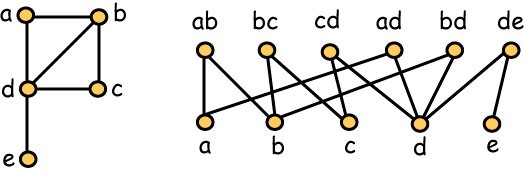
Inclusion poset of a graph.

Given a graph $G=(V,E)$ its inclusion poset $Inc(G)$ is a poset on $V \cup E$ such that $x < y$ if and only if $x$ is a vertex incident to an edge $y$. In 1989, W. Schnyder gave a new characterization of planar graphs [Sch] : $G$ is planar iff $Inc(G)$ has dimension at most 3. Here the dimension is the poset dimension, also known as Dushnik-Miller dimension. This is proved by showing that every planar triangulation admits a 3-realizer, also known as Schnyder wood (we do not define this here). Note that a triangulation usually admits several 3-realizers.

In [Bon] (see also [BB]) the author showed a bijection between the 3-realizers on $n$ vertices and pairs of non-crossing Dyck paths of length $2n-6$. During this internship the student will consider graphs admitting a 4-realizer (see [Oss] for properties of the graphs admitting a $d$-realizer), and the goal will be to study possible extensions of the previous result. For example, is there a bijection between 4-realizers and pairs of non-crossing orthogonal surfaces (a 3D-generalization of Dyck paths). This study will require some programing to enumerate the 4-realizers (of bounded size) and generalizations of Dyck paths.

References

[BB] O. Bernardi and N. Bonichon, Catalan’s intervals and realizers of triangulations, JCTA 116(1), 55-75, 2009.

[Bon] N. Bonichon, A bijection between realizers of maximal plane graphs and pairs of non-crossing dyck paths, Discrete Math., 298, 104-114, 2005.

[Oss] P. Ossona de Mendez, Geometric realization of simplicial complexes, LNCS 1731 (1999), 323-332.

[Sch] W. Schnyder, Planar graphs and poset dimension, Order 5, 323-343, 1989.