Context
Even the advent of new technologies of sequencing, large genomes still need to be assembled from millions of sequencing reads (usually much shorter than the genome itself). In other words, one gets as input a set of strings (the sequencing reads) and wishes to find a string (i.e. the genome) that contains each of the input strings, and is as short as possible. The final string containing the others is called a superstring. In computer science, computing a shortest linear superstring is a classical question studied since the 80’s.
From the computational viewpoint, finding a shortest superstring is known to be hard to solve (NP-hard even on a binary alphabet) and to approximate (Max-SNP hard). The research in the last 25 years has mainly focused on algorithms for finding approximate solutions in polynomial time. Despite these efforts, questions related to superstrings are far from fully understood. As intuition, the simple greedy algorithm, an algorithm that iteratively updates the input set by merging two maximally overlapping strings until one string is left, was conjectured to approximate the length of the shortest superstring with ratio of 2 in the 80’s, but this still remains to be proven.
Some top computer science researchers have worked on the tricky questions on superstrings like Ming Li (Univ. of Waterloo, Canada), Dan Gusfield (Univ. of California, Davis, USA), Max Crochemore (King’s College London, UK), Avril Blum (Carnegie Mellon Univ.), Tao Jiang (University of California, Riverside) or Esko Ukkonen (Univ. Helsinki) among others. Nevertheless, superstring questions seem to conceal important and complex issues of both combinatorial and computational nature. A lot remains to be investigated.
Objectives
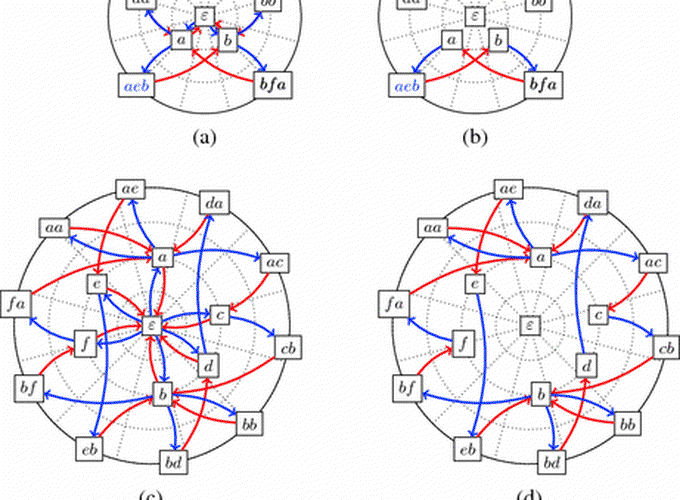
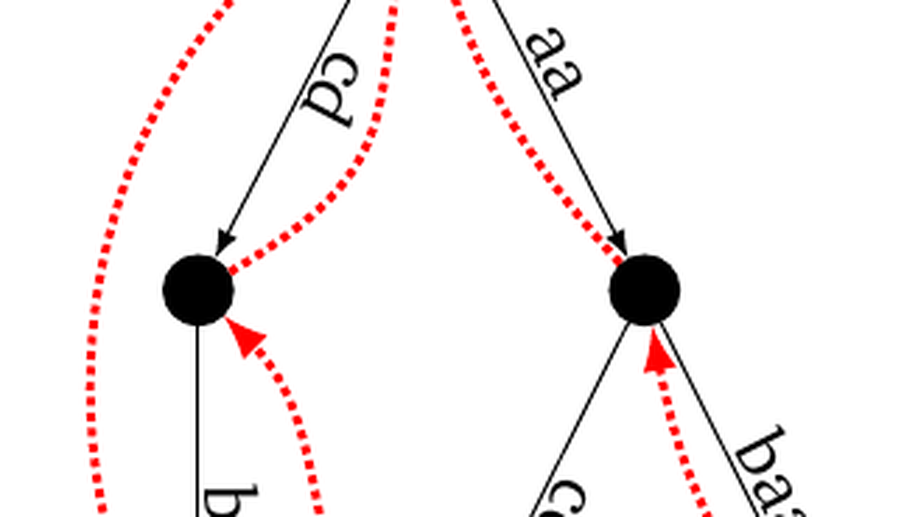
In this project from 2014 on, we investigate several superstring questions from a theoretical point of view, as well on their practical issues.
For instances,
- what if the sought superstring could be cyclic instead of linear?
- what if one seeks for a set of cyclic strings that collectively contains the input strings?
- what if one requires several copies of the input strings in the final superstring?
- what if one allow degenerate strings as input?
Considering aspects of superstrings that were disregarded in the literature, we exhibited new algorithms and graphs to compute superstrings, and uncovered novel, surprising properties on theses questions. This work led to several publications in computer science journals and international conferences, where we describe our findings.
Team
- Bastien Cazaux (Postdoctoral fellow)
- Samuel Juhel (Master student)
- Rodrigo Cánovas (Postdoctoral fellow, now Univ. Australia)
External collaborators
- Gustavo Sacomoto (Google)
- Prof. Kunsoo Park (Seoul National Univ.)