Abstract
Finding the correct position of new sequences within an established phylogenetic tree is an increasingly relevant problem in evolutionary bioinformatics and metagenomics. Recently, alignment-free approaches for this task have been proposed. One such approach is based on the concept of phylogenetically-informative k-mers or phylo- k-mers for short. In practice, phylo- k-mers are inferred from a set of related reference sequences and are equipped with scores expressing the probability of their appearance in different locations within the input reference phylogeny. Computing phylo- k-mers, however, represents a computational bottleneck to their applicability in real-world problems such as the phylogenetic analysis of metabarcoding reads and the detection of novel recombinant viruses. Here we consider the problem of phylo- k-mer computation: how can we efficiently find all k-mers whose probability lies above a given threshold for a given tree node? We describe and analyze algorithms for this problem, relying on branch-and-bound and divide-and-conquer techniques. We exploit the redundancy of adjacent windows of the alignment to save on computation. Besides computational complexity analyses, we provide an empirical evaluation of the relative performance of their implementations on simulated and real-world data. The divide-and-conquer algorithms are found to surpass the branch-and-bound approach, especially when many phylo- k-mers are found.
Publication
IEEE/ACM Transactions on Computational Biology and Bioinformatics
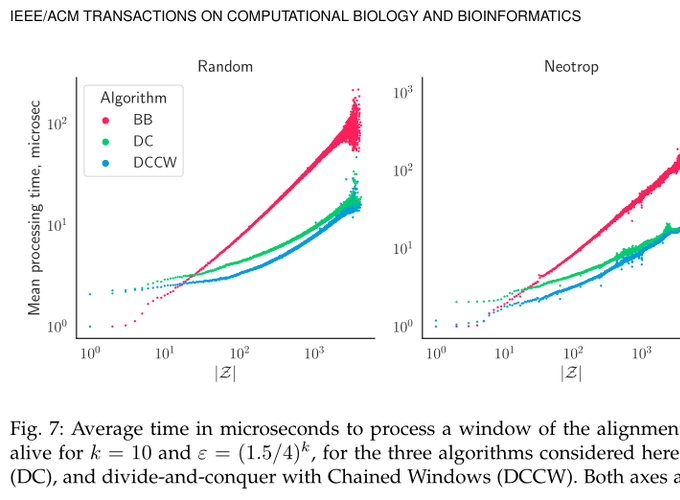 Figure 7: Average running time in microseconds to process a window of an alignement plotted against the number of phylo-k-mers alive for k=10 and epsilon=(1.5/4)^k, for the three algorithms considered here: branch-and-bound (BB), divide-and-conquer (DC), and divide-and-conquer with Chained Windows (DCCW). Both axes are in log-scale.
Figure 7: Average running time in microseconds to process a window of an alignement plotted against the number of phylo-k-mers alive for k=10 and epsilon=(1.5/4)^k, for the three algorithms considered here: branch-and-bound (BB), divide-and-conquer (DC), and divide-and-conquer with Chained Windows (DCCW). Both axes are in log-scale.