The DeepPulseNeuro project was recognized at the 2025 edition of...
Read MoreThe Laboratoire d’Informatique, de Robotique et de Microélectronique de Montpellier (Laboratory of Computer Science, Robotics and Microelectronics of Montpellier) is a major multi-disciplinary French research center located in the South of France. It is affiliated with the University of Montpellier and the French National Center for Scientific Research (Centre National de la Recherche Scientifique, CNRS). It conducts research in Computer Science, Microelectronics and Robotics and is organized along 3 departments comprising 19 international research teams assisted by central services personnel… next



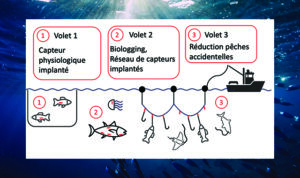
The ENTREMETS project honored by the CNRS MITI
The ENTREMETS project – Development of sensors and sensor networks...
Read MoreMichel Robert joins the Montpellier Academy of Sciences and Letters
The official inauguration ceremony for Michel Robert at the Montpellier...
Read MoreSpotlight on LIRMM talent: Paul Leloup featured in the “Rouages” series
As part of the LIRMM research support department since 2019,...
Read MoreThe executive team