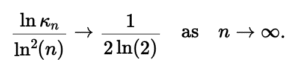Les technologies de séquençage permettent d’obtenir la séquence (suite de symboles) qui représente une molécule d’ADN, d’ARN ou encore de protéines. La bioinformatique permet d’analyser ces séquences grâce à des algorithmes issus du domaine d’algorithmique du texte (stringology en anglais). Avec la révolution des technologies de séquençage à haut débit, le volume de séquences à traiter explose. Les projets de génomique ou de transcriptomique produisent chacun des centaines de millions de séquences (aussi appelées lectures). Nous concevons des algorithmes performants pour analyser les séquences biologiques à grande échelle. Ces algorithmes sont implantés dans des logiciels de bioinformatique qui allient efficacité et sensibilité, par exemple pour
- corriger les erreurs de séquençage (LoRDEC, LoRMA)
- trouver la position d’une séquence dans un génome (CRAC, MPSCAN)
- comparer des génomes (QOD, YOC)
- pour l’assemblage et l’échaffaudage de génomes (SAVAGE, SCAFFOLDER)
- pour la recherche de motif de fixation de protéines.
Ces logiciels sont diffusés au travers de notre plateforme de bioinformatique ATGC. Ils sont ensuite utilisés sur des données réelles pour des études en biologie moléculaire, en biodiversité, en biologie évolutive. Par exemple,
- le projet du génome d’une micro-algue marine
- étudier la réplication du génome des vertébrés
- ou les transcriptomes humain, d’animaux ou de plantes.
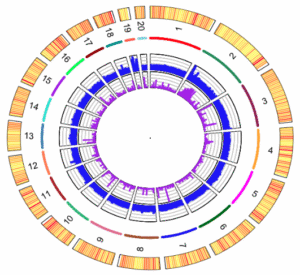
La Figure 1 présente un résultat d’application dans un projet génomique : Visualisation circulaire des chromsomes du génome de O. tauri une pico-algue présente dans toutes les mers du globe. (Blanc-Mathieu et al., BMC Genomics, 15:1103 10.1186/1471-2164-15-1103, 2014)
L’efficacité de ces outils provient souvent de l’utilisation de structures de données d’indexation, comme l’arbre des suffixes, la transformée de Burrows-Wheeler, ou les arbres à ondelettes. Par exemple, nous avons proposé des algorithmes pour
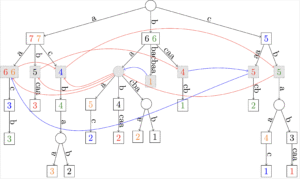
- construire de graphes d’assemblage (Figure 2)
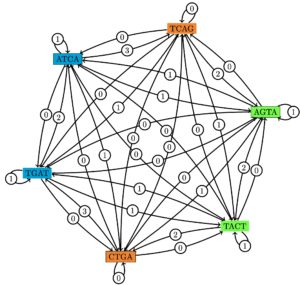
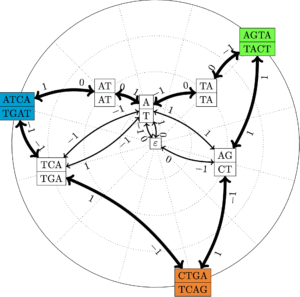
- calculer des superchaines (Figures 3, 4)
- comparer des séquences à des graphes.
Figure 2 : Représentation d’un graphe de De Bruijn dans une structure d’arbre des suffixes généralisée. (Cazaux et al., J. Computer System & Sciences, http://dx.doi.org/10.1016/j.jcss.2016.06.008, 2016).
La plupart des questions informatiques appartiennent à la catégorie des problèmes d’optimisation et sont difficiles. On cherche alors des algorithmes d’approximation et on étudie leur ratio d’approximation qui mesure une distance à une solution optimale. Les algorithmes gloutons en sont un exemple.
Figure 3 : Pour un ensemble de trois séquences P := { ATCA, AGTA, CTGA } et leurs complémentaires inversés, représentation du (classique) graphe des chevauchements (Cazaux et al., Data Compression Conf. 2016).
Figure 4 : Pour un ensemble de trois séquences P := { ATCA, AGTA, CTGA } et leurs complémentaires inversés, représentations du graphe des chevauchements, qui contient les mêmes informations que le graphe de chevauchements, mais utilise une mémoire espace linéaire (Cazaux et al., Data Compression Conf. 2016).
Nous avons défini un nouveau type de graphe pour représenter l’ensemble des chevauchements d’un ensemble de mots.
En pratique, les assemblages de génome utilisent des structures de données d’indexation pour calculer les chevauchements entre séquences, et inférer des superchaînes. Nous avons étudié les liens entre plusieurs graphes de chevauchement entre séquences et les structures permettant d’indexer ces séquences. Nous proposons des algorithmes pour construire les graphes directement à partir des index pour le graphe de chevauchement et le graphe de De Bruijn (Cazaux et al. JCSS, 2019). Cela nous a conduit à proposer un graphe plus compact et plus informatif, le HOG (Cazaux et Rivals, IPL, 2020) dont nous avons prouvé qu’il est pertinent en pratique (Cazaux et al. SEA, 2018). Un article en collaboration avec l’Université de Séoul et l’entreprise Samsung exhibe un algorithme linéaire et donc optimal pour construire le HOG (Cazaux et al, CPM, 2021). Ces résultats éclaircissent le comportement des assembleurs à l’aide de propriétés théoriques et donnent des pistes pour les améliorer (Cazaux, Rivals, CPM, 2019).
Notre algorithme linéaire pour la construction du HOG a été utilisé dans un nouveau logiciel de conception de vaccin à base de peptides, HOGVAX, et qui a reçu le prix du meilleur article à la conférence RECOMB 2023 (Schulte et al, Cell Systems, 2023).
Les travaux sur les graphes de chevauchements de séquences ainsi que sur le graphe hiérarchique de chevauchements nous ont poussé à travailler sur la combinatoire des chevauchements de mots. En effet lorsque deux mots se chevauchent ou un mot s’auto-chevauche, c’est à dire lorsqu’un préfixe d’un mot est identique au suffixe d’un autre, plusieurs chevauchements sont possibles mais pas tous. Il existe des contraintes intrinsèques qui limitent les combinaisons de chevauchements possibles.
Dans un premier temps, on peut examiner le cas des auto-chevauchements : l’ensemble des chevauchements d’un mot sur lui même est représentée soit par son ensemble de périodes (un sous-ensemble des entiers entre zéro et n – 1 où n est la longueur du mot), soit en binaire par son autocorrélation (Guibas te Odlyzko, JCTA, 1981). Depuis le travail de Guibas et Odlyzko en 1981, il subsistait une conjecture sur le nombre d’ensemble de périodes des mots de longueur et grâce à une nouvelle approche nous avons résolu cette conjecture (Rivals, Wang, Sweering, ICALP, 2023) (–,Algorithmica, 2025).
Cette étude concerne la combinatoire des chevauchements d’une séquence de lettres, autrement dit d’un mot. Un mot de longueur n se chevauche si un de ses préfixes égale un de ses suffixes. Par ex., le mot abracadabra contient deux chevauchements (abra et a), donc un décalage de ou de l’amènent à se chevaucher. Ces décalages sont les périodes du mot. En 1981, Guibas et Odlyzko ont étudié le nombre, noté Kn, d’ensembles de périodes possibles pour les mots de longueur n (Guibas te Odlyzko, JCTA, 1981) et conjecturé que
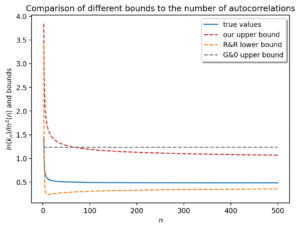
En 2003, en établissant un lien entre les ensembles de périodes et les partitions binaires des entiers, deux bornes inférieures pour le ratio ln Kn/ln2(n) ont été prouvées (Rivals et Rahmann, JCTA, 2003). En outre, les nombreuses études sur la combinatoire des tables de préfixes ou de bords (structures dont on déduit aisément l’ensemble des périodes) (Duval et al. 2005, Holub et al., 2006, Bland et al. CPM, 2013, Clement et Giambruno, 2015) n’ont pas permis de résoudre la conjecture de 1981. En exploitant le concept d’ensemble de périodes irréductibles, nous avons démontré une nouvelle borne supérieure pour ce ratio, ce qui a permis de clore la conjecture de Guibas et Odlyzko (Rivals, Wang, Sweering, ICALP, 2023). La figure 1 montre les bornes inférieures et supérieures ainsi que les valeurs réelles. L’ensemble de périodes est l’élément clef qui contrôle la probabilité d’absence d’un mot dans un texte aléatoire. Il est utilisé pour la construction de code, le test de générateur pseudo-aléatoire, ou la recherche de motifs (Lossers, SIAM Rev, 1995, Percus et Whitlock, ACM Trans. Modeling and Computer Simulation, 1995, Robin et al. CUP 2006).
Par ailleurs, avec la thèse de Pengfei Wang, nous avons étudié la question plus complexe des chevauchements entre deux mots. La combinaison de tous les chevauchements entre deux mots donnés peut être représentée en binaire par leur corrélation (Guibas te Odlyzko, JCTA, 1981 a et b). Nous avons dénombré les différentes corrélations possibles pour les mots de même taille et montré que leur nombre, noté δₙ, est une somme des nombres d’ensembles de périodes (Rivals, Wang, Sweering, ICALP, 2023). Il s’ensuit que le ratio ln δₙ/ln2(n) converge de la même manière que ln Kₙ/ln2 (n).
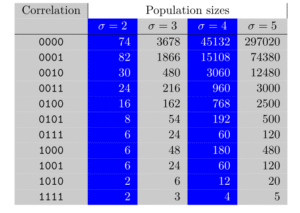
Puis, nous avons proposé en 2024 des algorithmes pour calculer le nombre de paires de mots, pour une taille d’alphabet donnée, qui respectent une corrélation donnée ; on appelle ce nombre la taille de population d’une corrélation. Cela nous a permis de résoudre deux questions ouvertes sur les mots de longueur par Gabric en 2022 (Gabric, IEEE Trans on Information Theory, 2022) :
- Q1: dénombrer le nombre de paires de mots ayant un plus long bord de longueur i, pour i satisfaisant 0 < i < n.
- Q2: calculer l’espérance de la longueur du plus long bord entre toutes les paires de mots de longueur n ?
Des exemples de taille de population sont données figure 2. Ces travaux sont présentés dans la thèse de P. Wang (Wang, PhD thesis, 2024) et dans un article (Rivals et Wang, COCOON, 2025).
- Daniel Gabric. Mutual borders and overlaps. IEEE Transactions on Information Theory, 68(10):6888–6893, 2022. https://doi.org/10.1109/TIT.2022.3167935.
- Leonidas J. Guibas and Andrew M. Odlyzko. Periods in strings. Journal of Combinatorial Theory, Series. A, 30:19–42, 1981. https://doi.org/10.1016/0097-3165(81)90038-8.
- Leonidas J. Guibas and Andrew M. Odlyzko. String overlaps, pattern matching, and nontransitive games. Journal of Combinatorial Theory, Series A, 30(2):183–208, 1981. https://doi.org/10.1016/0097-3165(81)90005-4.
- Eric Rivals and Sven Rahmann. Combinatorics of periods in strings. Journal of Combinatorial Theory, Series A, 104(1):95–113, 2003. https://doi.org/10.1016/s0097-3165(03)00123-7.
- Eric Rivals, Michelle Sweering, and Pengfei Wang. Convergence of the Number of Period Sets in Strings. In Kousha Etessami, Uriel Feige, and Gabriele Puppis, editors, 50th International Colloquium on Automata, Languages, and Programming (ICALP 2023), volume 261 of Leibniz International Proceedings in Informatics (LIPIcs), pages 100:1–100:14, Dagstuhl, Germany, 2023. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. https://doi.org/10.4230/LIPIcs.ICALP.2023.100.
- Eric Rivals, Michelle Sweering, and Pengfei Wang. Convergence of the number of period sets in strings. Algorithmica, 87:690–711, February 2025. https://doi.org/10.1007/s00453-025-01295-y.
- Stéphane Robin, François Rodolphe, and Sophie Schbath. DNA, Words and Models. Cambrigde University Press, 2005.
- Sara C. Schulte, Alexander T. Dilthey, Gunnar W. Klau. HOGVAX: Exploiting epitope overlaps to maximize population coverage in vaccine design with application to SARS-CoV-2. Cell Systems 14 (2023). https://doi.org/10.1016/j.cels.2023.11.001
- William F. Smyth. Computating Pattern in Strings. Pearson Addison Wesley, 2003.
- Pengfei Wang. On some computational questions regarding string overlaps. Université de Montpellier, 2024. English. tel-05123306.